Automata Theory 简明教程

Ambiguity in Context-Free Grammars

如果某个无上下文文法 G 对于某个字符串 w ∈ L(G) 有多个派生树，则称其为 ambiguous grammar 。从该文法生成的某个字符串存在多个最右或最左派生。

Problem

检查产生规则为 −

X → X+X | X*X |X| a

的文法 G 是否模糊。

Solution

让我们找出字符串“a+a*a”的派生树。它有两个最左派生。

Derivation 1 −X → X+X → a X → a X*X → a+a*X → a+a*a

Parse tree 1 −

parse tree1

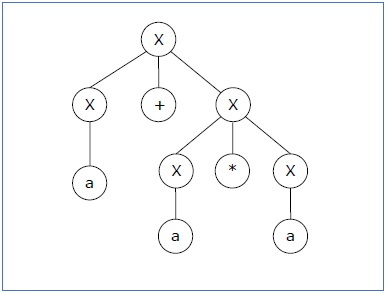
Derivation 2 − X → X*X → X+X*X → a+ X*X → a+a*X → a+a*a

Parse tree 2 −

parse tree2

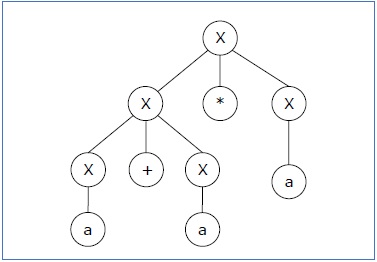
由于对于单个字符串“a+a*a”有两个解析树，文法 G 是模糊的。