Automata Theory 简明教程

Arden’s Theorem

为了找出有限自动机的正则表达式，我们使用 Arden 定理以及正则表达式的性质。

In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.

Statement -

Statement −

设 P 和 Q 是两个正则表达式。

Let P and Q be two regular expressions.

如果 P 不包含 null 字符串，则 R = Q + RP 具有唯一解 R = QP *

If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*

Proof −

R = Q + (Q + RP)P [在代入了 R = Q + RP 之后]

R = Q + (Q + RP)P [After putting the value R = Q + RP]

Q + QP + RPP

当我们不断递归地代入 R 的值时，我们得到以下方程 -

When we put the value of R recursively again and again, we get the following equation −

R = Q + QP + QP2 + QP3…..

R = Q (ε + P + P2 + P3 + …. )

R = QP* [因为 P* 表示 (ε + P + P2 + P3 + ….) ]

R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]

因此得证。

Hence, proved.

Assumptions for Applying Arden’s Theorem

The transition diagram must not have NULL transitions
It must have only one initial state

Method

Step 1 - 对于所有具有 n 个状态的 DFA 状态（初始状态为 q1），创建以下形式的方程。

Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.

q1 = q1R11 + q2R21 + … + qnRn1 + ε

q2 = q1R12 + q2R22 + … + qnRn2

…………………………

qn = q1R1n + q2R2n + … + qnRnn

Rij 表示从 qi 到 qj 的边的标签集合，如果不存在这样的边，则 Rij = ∅

Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅

Step 2 — 求解这些方程式，以 Rij 的形式获得最终状态方程式

Step 2 − Solve these equations to get the equation for the final state in terms of Rij

Problem

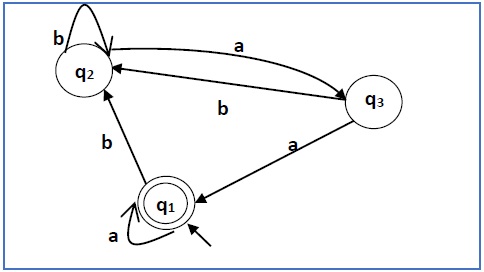
构造与以下给定自动机相对应的正则表达式 −

Construct a regular expression corresponding to the automata given below −

Solution −

此处初始状态和最终状态为 q1 。

Here the initial state and final state is q1.

三个状态 q1、q2 和 q3 的方程式如下 −

The equations for the three states q1, q2, and q3 are as follows −

q1 = q1a + q3a + ε（ε 移动是因为 q1 是初始状态 0

q1 = q1a + q3a + ε (ε move is because q1 is the initial state0

q2 = q1b + q2b + q3b

q3 = q2a

现在，我们将求解这三个方程式 −

Now, we will solve these three equations −

q2 = q1b + q2b + q3b

q1b + q2b + (q2a)b (Substituting value of q3)

q1b + q2(b + ab)

q1b (b + ab)* (Applying Arden’s Theorem)

q1 = q1a + q3a + ε

q1a + q2aa + ε (Substituting value of q3)

q1a + q1b(b + ab*)aa + ε (Substituting value of q2)

q1(a + b(b + ab)*aa) + ε

ε (a+ b(b + ab)aa)

(a + b(b + ab)aa)

因此，正则表达式为 (a + b(b + ab) aa) 。

Hence, the regular expression is (a + b(b + ab)aa).

Problem

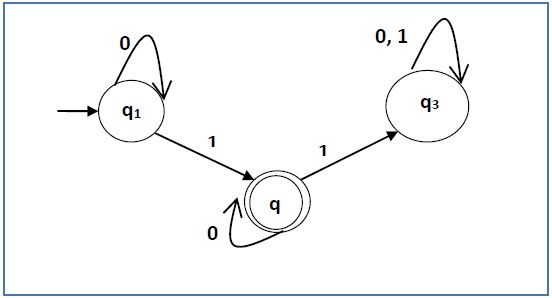
构造与以下给定自动机相对应的正则表达式 −

Construct a regular expression corresponding to the automata given below −

Solution −

此处初始状态为 q1，最终状态为 q2

Here the initial state is q1 and the final state is q2

现在我们写下方程式 −

Now we write down the equations −

q1 = q10 + ε

q2 = q11 + q20

q3 = q21 + q30 + q31

现在，我们将求解这三个方程式 −

Now, we will solve these three equations −

q1 = ε0* [，εR = R]

q1 = ε0* [As, εR = R]

所以，q1 = 0*

So, q1 = 0*

q2 = 0*1 + q20

所以，q2 = 0*1(0)* [由艾登定理]

So, q2 = 0*1(0)* [By Arden’s theorem]

因此，正则表达式为 0*10*。

Hence, the regular expression is 0*10*.