Automata Theory 简明教程

DFA Complement

如果 (Q, ∑, δ, q0, F) 是接受语言 L 的 DFA，则可以通过将接受状态与非接受状态以及反之互换来获得 DFA 的补集。

If (Q, ∑, δ, q0, F) be a DFA that accepts a language L, then the complement of the DFA can be obtained by swapping its accepting states with its non-accepting states and vice versa.

我们将举例并在下面详细说明 −

We will take an example and elaborate this below −

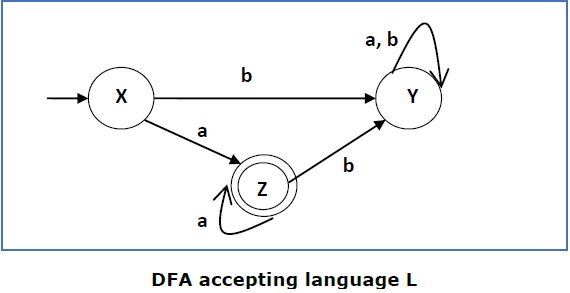
此 DFA 接受语言

This DFA accepts the language

L = {a, aa, aaa , …………. }

在字母表上

over the alphabet

∑ = {a, b}

所以，RE = a+。

So, RE = a+.

现在，我们将它的接受状态与其不接受状态互换，反之亦然，并且将获得以下状态：

Now we will swap its accepting states with its non-accepting states and vice versa and will get the following −

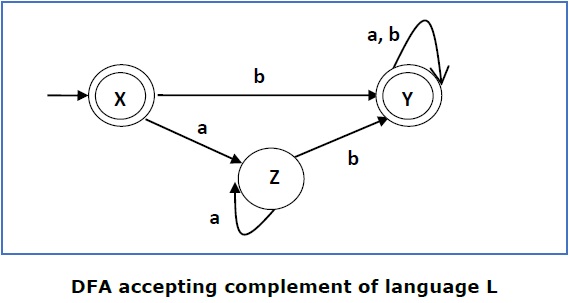
此 DFA 接受语言

This DFA accepts the language

Ľ = {ε, b, ab、bb、ba、…………… }

Ľ = {ε, b, ab ,bb,ba, …………… }

在字母表上

over the alphabet

∑ = {a, b}

Note - 如果我们希望对 NFA 求补，我们必须首先将其转换为 DFA，然后像在前面的方法中一样交换状态。

Note − If we want to complement an NFA, we have to first convert it to DFA and then have to swap states as in the previous method.