Automata Theory 简明教程

Deterministic Finite Automaton

有限自动机可分为两类：

Finite Automaton can be classified into two types −

  1. Deterministic Finite Automaton (DFA)

  2. Non-deterministic Finite Automaton (NDFA / NFA)

Deterministic Finite Automaton (DFA)

在 DFA 中，对于每个输入符号，都可以确定机器将移动到的状态。因此，它被称为 Deterministic Automaton 。由于它具有有限数量的状态，因此机器被称为 Deterministic Finite Machine 或 Deterministic Finite Automaton. 。

In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.

Formal Definition of a DFA

DFA 可以表示为 5 元组 (Q, ∑, δ, q0, F)，其中 −

A DFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where −

  1. Q is a finite set of states.

  2. ∑ is a finite set of symbols called the alphabet.

  3. δ is the transition function where δ: Q × ∑ → Q

  4. q0 is the initial state from where any input is processed (q0 ∈ Q).

  5. F is a set of final state/states of Q (F ⊆ Q).

Graphical Representation of a DFA

DFA 由称为 state diagram 的有向图表示。

A DFA is represented by digraphs called state diagram.

  1. The vertices represent the states.

  2. The arcs labeled with an input alphabet show the transitions.

  3. The initial state is denoted by an empty single incoming arc.

  4. The final state is indicated by double circles.

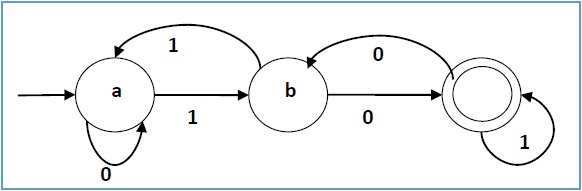
Example

让确定性有限自动机为→

Let a deterministic finite automaton be →

  1. Q = {a, b, c},

  2. ∑ = {0, 1},

  3. q0 = {a},

  4. F = {c}, and

过渡函数 δ 如下表所示−

Transition function δ as shown by the following table −

Present State

Next State for Input 0

Next State for Input 1

a

a

b

b

c

a

c

b

c

它的图形表示如下−

Its graphical representation would be as follows −

dfa graphical representation