Automata Theory 简明教程

Construction of an FA from an RE

我们可以使用汤普森构建法发现一个由正则表达式构造的有穷自动机。我们将正则表达式简化为最小的正则表达式，然后将这些表达式转换为 NFA，最后转换为 DFA。

We can use Thompson’s Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.

一些基本的 RA 表达式为：

Some basic RA expressions are the following −

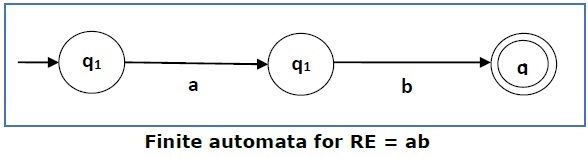
Case 1 －对于正则表达式“a”，我们可以构造以下 FA －

Case 1 − For a regular expression ‘a’, we can construct the following FA −

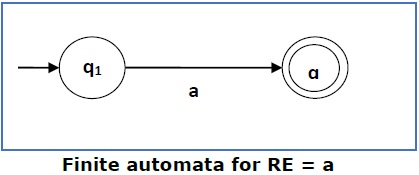
Case 2 − 对于正则表达式“ab”，我们可以构建以下 FA −

Case 2 − For a regular expression ‘ab’, we can construct the following FA −

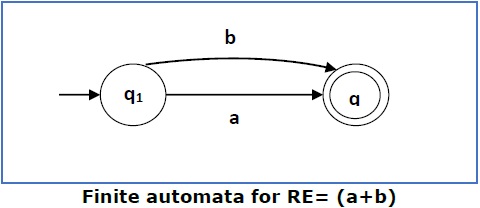
Case 3 − 对于正则表达式 (a+b)，我们可以构建以下 FA −

Case 3 − For a regular expression (a+b), we can construct the following FA −

Case 4 − 对于正则表达式 (a+b)*，我们可以构建以下 FA −

Case 4 − For a regular expression (a+b)*, we can construct the following FA −

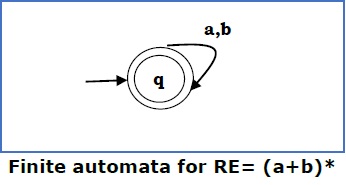
Method

Step 1 根据给定的正则表达式构建一个带有空动作的 NFA。

Step 1 Construct an NFA with Null moves from the given regular expression.

Step 2 从 NFA 中删除空转换，并将其转换成等效的 DFA。

Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.

Problem

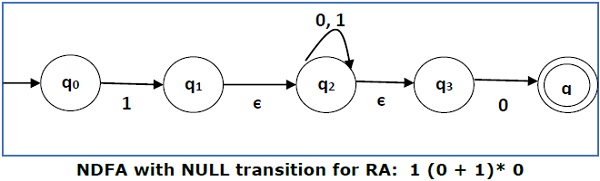
将以下 RA 转换成等效的 DFA − 1 (0 + 1)* 0

Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0

Solution

我们将三个表达式“1”、“(0 + 1)*”和“0”连接在一起

We will concatenate three expressions "1", "(0 + 1)*" and "0"

现在我们将删除 ε 转换。从 NDFA 中删除 ε 转换后，我们得到以下结果 −

Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

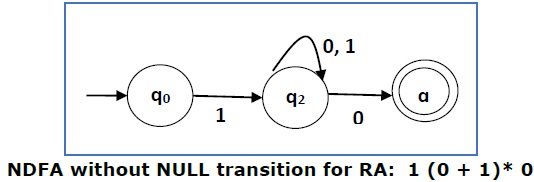
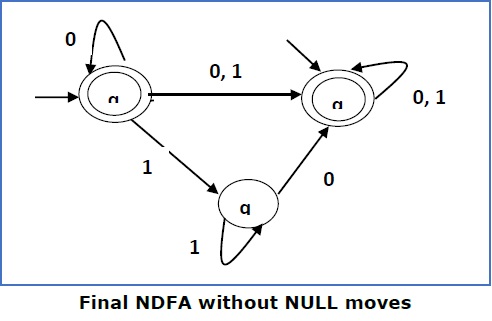
它是与 RE − 1 (0 + 1)* 0 相对应的 NDFA。如果你想将其转换成 DFA，只需应用第 1 章中讨论的 NDFA 到 DFA 的转换方法。

It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.

Finite Automata with Null Moves (NFA-ε)

带有空动作的有限自动机 (FA-ε) 不仅在从字母集合提供输入后进行转换，还可以在没有输入符号的情况下进行转换。这种没有输入的转换称为 null move 。

A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.

NFA-ε 由一个 5 元组（Q、∑、δ、q0、F）正式表示，其中包括

An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of

Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).

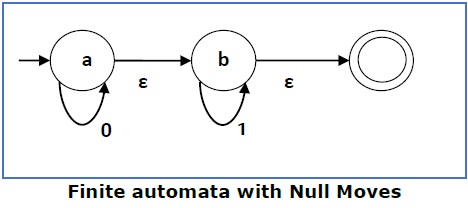
上述 (FA-ε) 接受一个字符串集合 − {0, 1, 01}

The above (FA-ε) accepts a string set − {0, 1, 01}

Removal of Null Moves from Finite Automata

如果在 NDFA 中，存在从顶点 X 到顶点 Y 的 ϵ 动作，我们可以使用以下步骤将其删除 −

If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −

Find all the outgoing edges from Y.
Copy all these edges starting from X without changing the edge labels.
If X is an initial state, make Y also an initial state.
If Y is a final state, make X also a final state.

Problem

将以下 NFA-ε 转换为没有空移动的 NFA。

Convert the following NFA-ε to NFA without Null move.

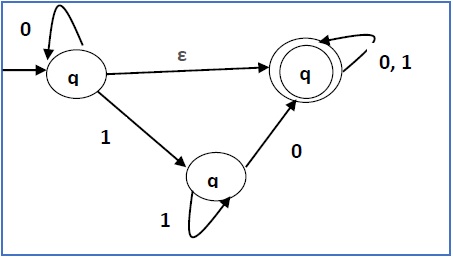
Solution

Step 1 -

Step 1 −

这里 ε 转换在 q1 和 q2 之间，所以让 q1 等于 X ，而 qf 等于 Y 。

Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.

这里从 qf 出发到 qf 的输出边针对输入 0 和 1。

Here the outgoing edges from qf is to qf for inputs 0 and 1.

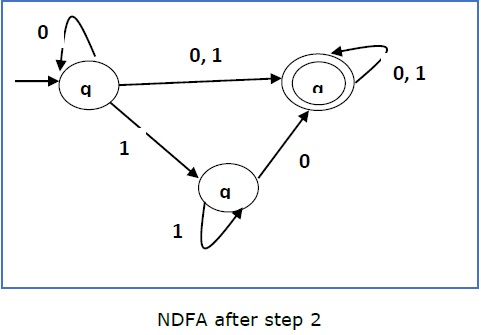
Step 2 -

Step 2 −

现在，我们将从 q1 复制所有这些边，而不会更改从 qf 分出的边，并获得以下 FA −

Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −

Step 3 -

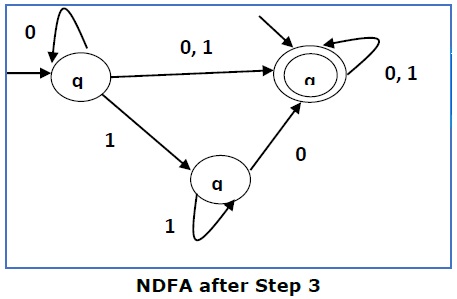
Step 3 −

这里 q1 是一个初始状态，所以我们也将 qf 设置为初始状态。

Here q1 is an initial state, so we make qf also an initial state.

因此 FA 变成 −

So the FA becomes −

Step 4 -

Step 4 −

这里 qf 是一个终止状态，因此我们也将 q1 设置为终止状态。

Here qf is a final state, so we make q1 also a final state.

因此 FA 变成 −

So the FA becomes −