Automata Theory 简明教程

Automata Theory - Quick Guide

Automata Theory Introduction

Automata – What is it?

术语“自动机”源自希腊语单词“αὐτόματα”，意思是“自作用”。自动机（复数形式为 Automata）是一种抽象的自驱动计算设备，它自动执行预定的操作序列。

The term "Automata" is derived from the Greek word "αὐτόματα" which means "self-acting". An automaton (Automata in plural) is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically.

具有有限状态数的自动机称为 Finite Automaton (FA) 或 Finite State Machine (FSM)。

An automaton with a finite number of states is called a Finite Automaton (FA) or Finite State Machine (FSM).

Formal definition of a Finite Automaton

自动机可以用 5 元组 (Q, ∑, δ, q0, F) 表示，其中 −

An automaton can be represented by a 5-tuple (Q, ∑, δ, q0, F), where −

Q is a finite set of states.
∑ is a finite set of symbols, called the alphabet of the automaton.
δ is the transition function.
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).

Related Terminologies

Alphabet

Definition − An alphabet is any finite set of symbols.
Example − ∑ = {a, b, c, d} is an alphabet set where ‘a’, ‘b’, ‘c’, and ‘d’ are symbols.

String

Definition − A string is a finite sequence of symbols taken from ∑.
Example − ‘cabcad’ is a valid string on the alphabet set ∑ = {a, b, c, d}

Length of a String

Definition − It is the number of symbols present in a string. (Denoted by |S|).
Examples − If S = ‘cabcad’, |S|= 6 If |S|= 0, it is called an empty string (Denoted by λ or ε)

Kleene Star

Definition − The Kleene star, ∑*, is a unary operator on a set of symbols or strings, ∑, that gives the infinite set of all possible strings of all possible lengths over ∑ including λ.
Representation − ∑* = ∑0 ∪ ∑1 ∪ ∑2 ∪……. where ∑p is the set of all possible strings of length p.
Example − If ∑ = {a, b}, ∑* = {λ, a, b, aa, ab, ba, bb,………..}

Kleene Closure / Plus

Definition − The set ∑+ is the infinite set of all possible strings of all possible lengths over ∑ excluding λ.
Representation − ∑+ = ∑1 ∪ ∑2 ∪ ∑3 ∪……. ∑+ = ∑* − { λ }
Example − If ∑ = { a, b } , ∑+ = { a, b, aa, ab, ba, bb,………..}

Language

Definition − A language is a subset of ∑* for some alphabet ∑. It can be finite or infinite.
Example − If the language takes all possible strings of length 2 over ∑ = {a, b}, then L = { ab, aa, ba, bb }

Deterministic Finite Automaton

有限自动机可分为两类：

Finite Automaton can be classified into two types −

Deterministic Finite Automaton (DFA)
Non-deterministic Finite Automaton (NDFA / NFA)

Deterministic Finite Automaton (DFA)

在 DFA 中，对于每个输入符号，都可以确定机器将移动到的状态。因此，它被称为 Deterministic Automaton 。由于它具有有限数量的状态，因此机器被称为 Deterministic Finite Machine 或 Deterministic Finite Automaton. 。

In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.

Formal Definition of a DFA

DFA 可以表示为 5 元组 (Q, ∑, δ, q0, F)，其中 −

A DFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where −

Q is a finite set of states.
∑ is a finite set of symbols called the alphabet.
δ is the transition function where δ: Q × ∑ → Q
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).

Graphical Representation of a DFA

DFA 由称为 state diagram 的有向图表示。

A DFA is represented by digraphs called state diagram.

The vertices represent the states.
The arcs labeled with an input alphabet show the transitions.
The initial state is denoted by an empty single incoming arc.
The final state is indicated by double circles.

Example

让确定性有限自动机为→

Let a deterministic finite automaton be →

Q = {a, b, c},
∑ = {0, 1},
q0 = {a},
F = {c}, and

过渡函数 δ 如下表所示−

Transition function δ as shown by the following table −

Present State

Next State for Input 0

Next State for Input 1

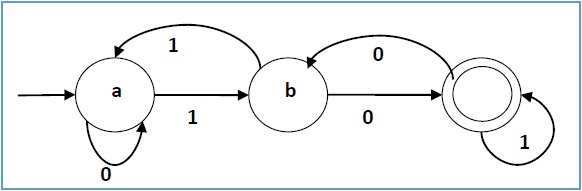
它的图形表示如下−

Its graphical representation would be as follows −

Non-deterministic Finite Automaton

在 NDFA 中，对于特定的输入符号，机器可以移动到机器中的任何状态组合。换句话说，无法确定机器移动到的确切状态。因此，它称为 Non-deterministic Automaton 。由于它有有限数量的状态，因此机器称为 Non-deterministic Finite Machine 或 Non-deterministic Finite Automaton 。

In NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine. In other words, the exact state to which the machine moves cannot be determined. Hence, it is called Non-deterministic Automaton. As it has finite number of states, the machine is called Non-deterministic Finite Machine or Non-deterministic Finite Automaton.

Formal Definition of an NDFA

NDFA 可以用 5 元组 (Q, ∑, δ, q0, F) 表示，其中−

An NDFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where −

Q is a finite set of states.
∑ is a finite set of symbols called the alphabets.
δ is the transition function where δ: Q × ∑ → 2Q (Here the power set of Q (2Q) has been taken because in case of NDFA, from a state, transition can occur to any combination of Q states)
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).

Graphical Representation of an NDFA: (same as DFA)

NDFA 由称为状态图的有向图表示。

An NDFA is represented by digraphs called state diagram.

The vertices represent the states.
The arcs labeled with an input alphabet show the transitions.
The initial state is denoted by an empty single incoming arc.
The final state is indicated by double circles.

Example

令非确定性有限自动机为→

Let a non-deterministic finite automaton be →

Q = {a, b, c}
∑ = {0, 1}
q0 = {a}
F = {c}

过渡函数 δ 如下所示−

The transition function δ as shown below −

Present State

Next State for Input 0

Next State for Input 1

a, c

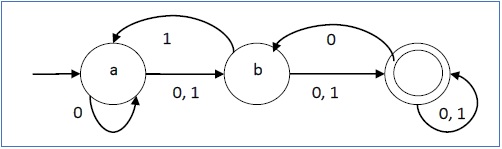
它的图形表示如下−

Its graphical representation would be as follows −

DFA vs NDFA

下表列出了 DFA 和 NDFA 之间的差异。

The following table lists the differences between DFA and NDFA.

DFA

NDFA

The transition from a state is to a single particular next state for each input symbol. Hence it is called deterministic.

The transition from a state can be to multiple next states for each input symbol. Hence it is called non-deterministic.

Empty string transitions are not seen in DFA.

NDFA permits empty string transitions.

Backtracking is allowed in DFA

In NDFA, backtracking is not always possible.

Requires more space.

Requires less space.

A string is accepted by a DFA, if it transits to a final state.

A string is accepted by a NDFA, if at least one of all possible transitions ends in a final state.

Acceptors, Classifiers, and Transducers

Acceptor (Recognizer)

计算布尔函数的自动机称为 acceptor 。接受器的所有状态要么接受要么拒绝给定的输入。

An automaton that computes a Boolean function is called an acceptor. All the states of an acceptor is either accepting or rejecting the inputs given to it.

Classifier

一个 classifier 有多于两个最终状态，并且在终止时给出单个输出。

A classifier has more than two final states and it gives a single output when it terminates.

Transducer

基于当前输入和/或先前状态生成输出的自动机称为 transducer 。转换器可以是两种类型：

An automaton that produces outputs based on current input and/or previous state is called a transducer. Transducers can be of two types −

Mealy Machine − The output depends both on the current state and the current input.
Moore Machine − The output depends only on the current state.

Acceptability by DFA and NDFA

当 DFA/NDFA 从初始状态开始在完整读取字符串后结束于接受状态（任何最终状态）时，一个字符串才会被 DFA/NDFA 接受。

A string is accepted by a DFA/NDFA iff the DFA/NDFA starting at the initial state ends in an accepting state (any of the final states) after reading the string wholly.

字符串 S 被 DFA/NDFA (Q, ∑, δ, q0, F) 接受，当且仅当

A string S is accepted by a DFA/NDFA (Q, ∑, δ, q0, F), iff

δ (q0, S) ∈ F*

δ(q0, S) ∈ F*

DFA/NDFA 接受的语言 L 是

The language L accepted by DFA/NDFA is

{S | S ∈ ∑ 并且 δ*(q0, S) ∈ F}*

{S | S ∈ ∑ and δ*(q0, S) ∈ F}*

如果一个字符串 S′ 不被 DFA/NDFA (Q, ∑, δ, q0, F) 所接受，则

A string S′ is not accepted by a DFA/NDFA (Q, ∑, δ, q0, F), iff

δ (q0, S′) ∉ F*

δ(q0, S′) ∉ F*

DFA/NDFA 所不接受的语言 L′（所接受语言 L 的补集）为

The language L′ not accepted by DFA/NDFA (Complement of accepted language L) is

{S | S ∈ ∑ and δ*(q0, S) ∉ F}*

Example

我们考虑图 1.3 中所示的 DFA。可以从 DFA 推导出可接受的字符串。

Let us consider the DFA shown in Figure 1.3. From the DFA, the acceptable strings can be derived.

上述 DFA 所接受的字符串：{0, 00, 11, 010, 101, ………..}

Strings accepted by the above DFA: {0, 00, 11, 010, 101, ………..}

上述 DFA 所不接受的字符串：{1, 011, 111, ……..}

Strings not accepted by the above DFA: {1, 011, 111, ……..}

NDFA to DFA Conversion

Problem Statement

设 X = (Qx, ∑, δx, q0, Fx) 是接受语言 L(X) 的 NDFA。我们必须设计一个等效 DFA Y = (Qy, ∑, δy, q0, Fy) ，使得 L(Y) = L(X) 。以下过程将 NDFA 转换为其等效 DFA −

Let X = (Qx, ∑, δx, q0, Fx) be an NDFA which accepts the language L(X). We have to design an equivalent DFA Y = (Qy, ∑, δy, q0, Fy) such that L(Y) = L(X). The following procedure converts the NDFA to its equivalent DFA −

Algorithm

Input − NDFA

Input − An NDFA

Output − 等效 DFA

Output − An equivalent DFA

Step 1 − 根据给定的 NDFA 创建状态表。

Step 1 − Create state table from the given NDFA.

Step 2 − 根据等效 DFA 的可能的输入字母创建一个空白状态表。

Step 2 − Create a blank state table under possible input alphabets for the equivalent DFA.

Step 3 − 标记为 q0 的 DFA 的起始状态（与 NDFA 相同）。

Step 3 − Mark the start state of the DFA by q0 (Same as the NDFA).

Step 4 − 找出对于每个可能的输入字母的状态 {Q0, Q1,… , Qn} 的组合。

Step 4 − Find out the combination of States {Q0, Q1,… , Qn} for each possible input alphabet.

Step 5 − 每次在输入字母列中生成一个新的 DFA 状态时，我们都必须重新应用步骤 4，否则转到步骤 6。

Step 5 − Each time we generate a new DFA state under the input alphabet columns, we have to apply step 4 again, otherwise go to step 6.

Step 6 − 包含 NDFA 的任何最终状态的状态是等效 DFA 的最终状态。

Step 6 − The states which contain any of the final states of the NDFA are the final states of the equivalent DFA.

Example

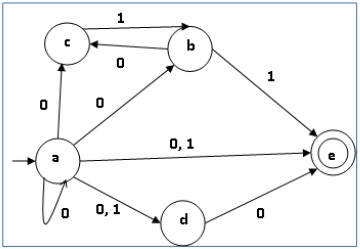
我们考虑下图所示的 NDFA。

Let us consider the NDFA shown in the figure below.

δ(q,0)

δ(q,1)

{a,b,c,d,e}

{d,e}

{c}

{e}

∅

{b}

{e}

∅

使用上述算法，我们可以找到其等效 DFA。DFA 的状态表如下所示。

Using the above algorithm, we find its equivalent DFA. The state table of the DFA is shown in below.

δ(q,0)

δ(q,1)

[a]

[a,b,c,d,e]

[d,e]

[a,b,c,d,e]

[b,d,e]

[d,e]

[e]

∅

[b,d,e]

[c,e]

[e]

∅

[c, e]

∅

[b]

[c]

[e]

[c]

∅

[b]

DFA 的状态图如下所示 −

The state diagram of the DFA is as follows −

DFA Minimization

DFA Minimization using Myhill-Nerode Theorem

Algorithm

Input - DFA

Input − DFA

Output - 最小化DFA

Output − Minimized DFA

Step 1 - 为所有状态对（Qi，Qj）绘制一个表格，不一定直接连接 [所有状态最初都未标记]

Step 1 − Draw a table for all pairs of states (Qi, Qj) not necessarily connected directly [All are unmarked initially]

Step 2 - 考虑DFA中每个状态对（Qi，Qj），其中Qi ∈ F且Qj ∉ F或反之亦然，并标记它们。[此处的F是结束状态集合]

Step 2 − Consider every state pair (Qi, Qj) in the DFA where Qi ∈ F and Qj ∉ F or vice versa and mark them. [Here F is the set of final states]

Step 3 - 重复此步骤，直至无法标记更多状态 -

Step 3 − Repeat this step until we cannot mark anymore states −

如果有未标记对（Qi，Qj），如果标记了对于某些输入字母的{δ（Qi，A），δ（Qi，A）}，则标记该对。

If there is an unmarked pair (Qi, Qj), mark it if the pair {δ (Qi, A), δ (Qi, A)} is marked for some input alphabet.

Step 4 - 组合所有未标记对（Qi，Qj），并使其成为缩小版DFA中的单个状态。

Step 4 − Combine all the unmarked pair (Qi, Qj) and make them a single state in the reduced DFA.

Example

让我们使用算法2来最小化下面显示的DFA。

Let us use Algorithm 2 to minimize the DFA shown below.

dfa minimizing using myhill nerode theorem

Step 1 - 为所有状态对绘制一张表格。

Step 1 − We draw a table for all pair of states.

Step 2 - 我们标记状态对。

Step 2 − We mark the state pairs.

✔

Step 3 - 我们将尝试使用绿色勾号标记状态对。如果我们将1输入到状态“a”和“f”，它将分别进入状态“c”和“f”。（c，f）已经标记，因此我们标记对（a，f）。现在，我们将1输入到状态“b”和“f”；它将分别转到状态“d”和“f”。（d，f）已经标记，因此我们标记对（b，f）。

Step 3 − We will try to mark the state pairs, with green colored check mark, transitively. If we input 1 to state ‘a’ and ‘f’, it will go to state ‘c’ and ‘f’ respectively. (c, f) is already marked, hence we will mark pair (a, f). Now, we input 1 to state ‘b’ and ‘f’; it will go to state ‘d’ and ‘f’ respectively. (d, f) is already marked, hence we will mark pair (b, f).

✔

在步骤3之后，我们得到了未标记的属性组合{a，b} {c，d} {c，e} {d，e}。

After step 3, we have got state combinations {a, b} {c, d} {c, e} {d, e} that are unmarked.

我们可以将{c，d} {c，e} {d，e}重新组合到{c，d，e}中

We can recombine {c, d} {c, e} {d, e} into {c, d, e}

因此，我们得到了两个组合状态为 - {a，b}和{c，d，e}

Hence we got two combined states as − {a, b} and {c, d, e}

因此，最终的最小化DFA将包含三个状态{f}、{a，b}和{c，d，e}

So the final minimized DFA will contain three states {f}, {a, b} and {c, d, e}

DFA Minimization using Equivalence Theorem

如果X和Y是DFA中的两个状态，如果它们不可区分，我们可以将这两个状态组合成{X，Y}。如果存在至少一个字符串S，则两个状态是可以区分的，即δ（X，S）和δ（Y，S）中的一个被接受，另一个不被接受。因此，当且仅当所有状态都可区分时，DFA才是最小的。

If X and Y are two states in a DFA, we can combine these two states into {X, Y} if they are not distinguishable. Two states are distinguishable, if there is at least one string S, such that one of δ (X, S) and δ (Y, S) is accepting and another is not accepting. Hence, a DFA is minimal if and only if all the states are distinguishable.

Algorithm 3

Step 1 - 所有状态 Q 被分为两个分区- final states 和 non-final states ，并由 P0 表示。分区中的所有状态都是0等价。获取计数器 k 并将其初始化为0。

Step 1 − All the states Q are divided in two partitions − final states and non-final states and are denoted by P0. All the states in a partition are 0th equivalent. Take a counter k and initialize it with 0.

Step 2 - 将k增加1。对于Pk中的每个分区，如果状态在Pk中是k可区分的，则将状态划分为两个分区。此分区X和Y中的两个状态在k-可区分，前提是有一个输入 S ，使得 δ(X, S) 和 δ(Y, S) 在（k-1）-可区分。

Step 2 − Increment k by 1. For each partition in Pk, divide the states in Pk into two partitions if they are k-distinguishable. Two states within this partition X and Y are k-distinguishable if there is an input S such that δ(X, S) and δ(Y, S) are (k-1)-distinguishable.

Step 3 - 如果Pk ≠ Pk-1，则重复步骤2，否则转到步骤4。

Step 3 − If Pk ≠ Pk-1, repeat Step 2, otherwise go to Step 4.

Step 4 − 将第 k 个等价集合组合起来，并将它们设定为化简 DFA 的新状态。

Step 4 − Combine kth equivalent sets and make them the new states of the reduced DFA.

Example

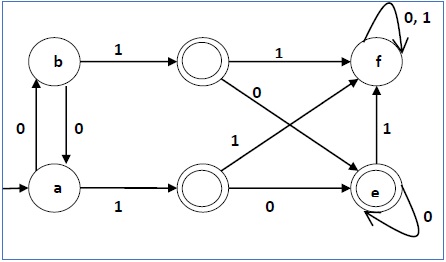
让我们思考下列 DFA −

Let us consider the following DFA −

δ(q,0)

δ(q,1)

让我们对上述 DFA 应用上述算法 −

Let us apply the above algorithm to the above DFA −

P0 = {(c,d,e), (a,b,f)}
P1 = {(c,d,e), (a,b),(f)}
P2 = {(c,d,e), (a,b),(f)}

因此，P1 = P2。

Hence, P1 = P2.

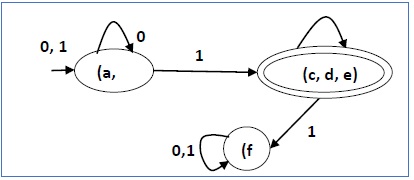
在化简后的 DFA 中有三个状态。化简后的 DFA 如下所示 −

There are three states in the reduced DFA. The reduced DFA is as follows −

δ(q,0)

δ(q,1)

(a, b)

(c,d,e)

(f)

Moore and Mealy Machines

有限自动机可以有对应于每个转换的输出。有两种类型的产生输出的有限状态机 -

Finite automata may have outputs corresponding to each transition. There are two types of finite state machines that generate output −

Mealy Machine
Moore machine

Mealy Machine

Mealy 机是一种 FSM，其输出取决于当前状态以及当前输入。

A Mealy Machine is an FSM whose output depends on the present state as well as the present input.

它可以用 6 元组 (Q，∑，O，δ，X，q0) 来描述，其中 -

It can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where −

Q is a finite set of states.
∑ is a finite set of symbols called the input alphabet.
O is a finite set of symbols called the output alphabet.
δ is the input transition function where δ: Q × ∑ → Q
X is the output transition function where X: Q × ∑ → O
q0 is the initial state from where any input is processed (q0 ∈ Q).

Mealy 机的状态表如下所示 -

The state table of a Mealy Machine is shown below −

Present state

Next state

input = 0

input = 1

State

Output

State

Output

→

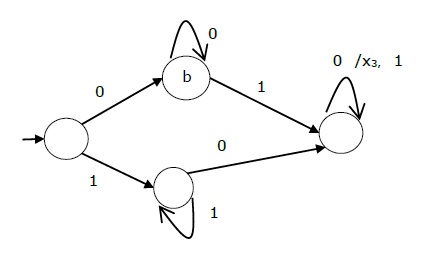
上述 Mealy 机的状态图如下 -

The state diagram of the above Mealy Machine is −

Moore Machine

Moore 机是一种 FSM，其输出仅取决于当前状态。

Moore machine is an FSM whose outputs depend on only the present state.

摩尔机可以用 6 元组 (Q, ∑, O, δ, X, q0) 来描述，其中 -

A Moore machine can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where −

Q is a finite set of states.
∑ is a finite set of symbols called the input alphabet.
O is a finite set of symbols called the output alphabet.
δ is the input transition function where δ: Q × ∑ → Q
X is the output transition function where X: Q → O
q0 is the initial state from where any input is processed (q0 ∈ Q).

摩尔机的状态表如下所示 -

The state table of a Moore Machine is shown below −

Present state

Next State

Output

Input = 0

Input = 1

→

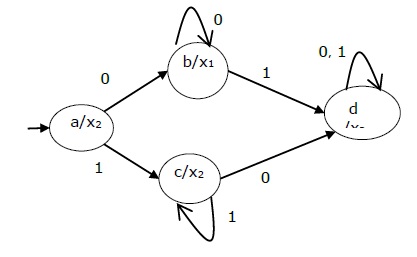
上述 Moore 机的状态图是 −

The state diagram of the above Moore Machine is −

Mealy Machine vs. Moore Machine

下表重点介绍了 Mealy 机与 Moore 机之间的不同点。

The following table highlights the points that differentiate a Mealy Machine from a Moore Machine.

Mealy Machine

Moore Machine

Output depends both upon the present state and the present input

Output depends only upon the present state.

Generally, it has fewer states than Moore Machine.

Generally, it has more states than Mealy Machine.

The value of the output function is a function of the transitions and the changes, when the input logic on the present state is done.

The value of the output function is a function of the current state and the changes at the clock edges, whenever state changes occur.

Mealy machines react faster to inputs. They generally react in the same clock cycle.

In Moore machines, more logic is required to decode the outputs resulting in more circuit delays. They generally react one clock cycle later.

Moore Machine to Mealy Machine

Algorithm 4

Input − Moore 机

Input − Moore Machine

Output − Mealy 机

Output − Mealy Machine

Step 1 − 采用一个空白的 Mealy 机转移状态表格式。

Step 1 − Take a blank Mealy Machine transition table format.

Step 2 − 将所有 Moore 机转移状态复制到此表格式中。

Step 2 − Copy all the Moore Machine transition states into this table format.

Step 3 − 检查 Moore 机状态表中的当前状态及其相应的输出；如果某个状态 Q 的输出为 m，将其复制到 Mealy 机状态表输出栏，Qi 出现于下一个状态的任何地方。

Step 3 − Check the present states and their corresponding outputs in the Moore Machine state table; if for a state Qi output is m, copy it into the output columns of the Mealy Machine state table wherever Qi appears in the next state.

Example

让我们考虑以下 Moore 机 −

Let us consider the following Moore machine −

Present State

Next State

Output

a = 0

a = 1

→

现在我们将算法 4 应用于将其转换到 Mealy 机。

Now we apply Algorithm 4 to convert it to Mealy Machine.

Step 1 & 2 −

Present State

Next State

a = 0

a = 1

State

Output

State

Output

→

Step 3 -

Step 3 −

Present State

Next State

a = 0

a = 1

State

Output

State

Output

⇒

Mealy Machine to Moore Machine

Algorithm 5

Input − Mealy 机

Input − Mealy Machine

Output − 穆尔机

Output − Moore Machine

Step 1 − 计算 Mealy 机状态表中每个状态 (Qi) 可用不同输出数。

Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.

Step 2 − 如果 Qi 的所有输出相同，复制状态 Qi。如果它有 n 个不同的输出，将 Qi 分解为 n 个状态，其中 Qin n = 0, 1, 2……。

Step 2 − If all the outputs of Qi are same, copy state Qi. If it has n distinct outputs, break Qi into n states as Qin where n = 0, 1, 2…….

Step 3 − 如果初始状态的输出为 1，在开头插入一个新的初始状态，其输出为 0。

Step 3 − If the output of the initial state is 1, insert a new initial state at the beginning which gives 0 output.

Example

让我们考虑一下以下 Mealy 机 −

Let us consider the following Mealy Machine −

Present State

Next State

a = 0

a = 1

Next State

Output

Next State

Output

→

此处，状态“a”和“d”分别仅提供输出 1 和 0，因此我们保留状态“a”和“d”。但状态“b”和“c”产生不同的输出（1 和 0）。因此，我们将 b 划分为 b0, b1 和 c 划分为 c0, c1 。

Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’. But states ‘b’ and ‘c’ produce different outputs (1 and 0). So, we divide b into b0, b1 and c into c0, c1.

Present State

Next State

Output

a = 0

a = 1

→

Introduction to Grammars

在术语的文学意义上，语法指示自然语言会话的语法规则。自英语、梵语、汉语等自然语言诞生以来，语言学就尝试定义语法。

n the literary sense of the term, grammars denote syntactical rules for conversation in natural languages. Linguistics have attempted to define grammars since the inception of natural languages like English, Sanskrit, Mandarin, etc.

形式语言理论在大幅度上发现计算机科学领域中的适用性。 Noam Chomsky 在 1956 年给出了语法的数学模型，该模型可有效书写计算机语言。

The theory of formal languages finds its applicability extensively in the fields of Computer Science. Noam Chomsky gave a mathematical model of grammar in 1956 which is effective for writing computer languages.

Grammar

语法 G 可以形式化为一个 4 元组 (N、T、S、P)，其中 −

A grammar G can be formally written as a 4-tuple (N, T, S, P) where −

N or VN is a set of variables or non-terminal symbols.
T or ∑ is a set of Terminal symbols.
S is a special variable called the Start symbol, S ∈ N
P is Production rules for Terminals and Non-terminals. A production rule has the form α → β, where α and β are strings on VN ∪ ∑ and least one symbol of α belongs to VN.

Example

语法 G1 −

Grammar G1 −

({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})

在此，

Here,

S, A, and B are Non-terminal symbols;
a and b are Terminal symbols
S is the Start symbol, S ∈ N
Productions, P : S → AB, A → a, B → b

Example

语法 G2 −

Grammar G2 −

(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε } )

(({S, A}, {a, b}, S,{S → aAb, aA → aaAb, A → ε } )

在此，

Here,

S and A are Non-terminal symbols.
a and b are Terminal symbols.
ε is an empty string.
S is the Start symbol, S ∈ N
Production P : S → aAb, aA → aaAb, A → ε

Derivations from a Grammar

字符串可以用语法中的产生式从其他字符串中派生。如果语法 G 有产生式 α → β ，我们可以说 x α y 在 G 中派生出 x β y 。此派生表示为 −

Strings may be derived from other strings using the productions in a grammar. If a grammar G has a production α → β, we can say that x α y derives x β y in G. This derivation is written as −

x α y ⇒G x β y

Example

让我们考虑语法 −

Let us consider the grammar −

G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε } )

可以派生的字符串包括 −

Some of the strings that can be derived are −

S ⇒ aAb 使用产生式 S → aAb

S ⇒ aAb using production S → aAb

⇒ aaAbb 使用产生式 aA → aAb

⇒ aaAbb using production aA → aAb

⇒ aaaAbbb 使用产生式 aA → aaAb

⇒ aaaAbbb using production aA → aaAb

⇒ aaabbb 使用产生式 A → ε

⇒ aaabbb using production A → ε

Language Generated by a Grammar

从语法中可以派生的所有字符串的集合称为从该语法生成的语言。语法 G 生成的语言是形式上由以下子集定义的

The set of all strings that can be derived from a grammar is said to be the language generated from that grammar. A language generated by a grammar G is a subset formally defined by

L(G)={W|W ∈ ∑ , S ⇒G *W }

L(G)={W|W ∈ ∑, S ⇒G *W}

如果 L(G1) = L(G2) ，语法 G1 等价于语法 G2 。

If L(G1) = L(G2), the Grammar G1 is equivalent to the Grammar G2.

Example

如果存在一个语法

If there is a grammar

G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}

此处 S 产生 AB ，我们可以用 a 替换 A ，用 b 替换 B 。这里，唯一可接受的字符串是 ab ，即

Here S produces AB, and we can replace A by a, and B by b. Here, the only accepted string is ab, i.e.,

L(G) = {ab}

Example

假设我们有以下语法 −

Suppose we have the following grammar −

G：N = {S、A、B} T = {a、b} P = {S → AB，A → aA|a，B → bB|b}

G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA|a, B → bB|b}

此语法生成的语言 −

The language generated by this grammar −

L(G) = {ab、a2b、ab2、a2b2、………}

L(G) = {ab, a2b, ab2, a2b2, ………}

{am bn | m ≥ 1 and n ≥ 1}

Construction of a Grammar Generating a Language

我们将考虑一些语言，并将其转换为生成那些语言的语法 G。

We’ll consider some languages and convert it into a grammar G which produces those languages.

Example

Problem − 假设，L (G) = {am bn | m ≥ 0 且 n > 0}。我们必须找出生成 L(G) 的语法 G 。

Problem − Suppose, L (G) = {am bn | m ≥ 0 and n > 0}. We have to find out the grammar G which produces L(G).

Solution

由于 L(G) = {am bn | m ≥ 0 且 n > 0}

Since L(G) = {am bn | m ≥ 0 and n > 0}

可以将可接受字符串集重写为 −

the set of strings accepted can be rewritten as −

L(G) = {b、ab、bb、aab、abb、…….}

L(G) = {b, ab,bb, aab, abb, …….}

这里，起始符号必须至少带有一个“b”，前面可以有任意数量的“a”，包括空串。

Here, the start symbol has to take at least one ‘b’ preceded by any number of ‘a’ including null.

为了接受字符串集 {b、ab、bb、aab、abb、……}，我们采用了以下产生式 −

To accept the string set {b, ab, bb, aab, abb, …….}, we have taken the productions −

S → aS，S → B，B → b 且 B → bB

S → aS , S → B, B → b and B → bB

S → B → b（已接受）

S → B → b (Accepted)

S → B → bB → bb（已接受）

S → B → bB → bb (Accepted)

S → aS → aB → ab（已接受）

S → aS → aB → ab (Accepted)

S → aS → aaS → aaB → aab（已接受）

S → aS → aaS → aaB → aab(Accepted)

S → aS → aB → abB → abb（已接受）

S → aS → aB → abB → abb (Accepted)

因此，我们可以证明 L(G) 中的每个字符串都由生成集合所生成的语义接受。

Thus, we can prove every single string in L(G) is accepted by the language generated by the production set.

因此语法 −

Hence the grammar −

G: ({S, A, B}, {a, b}, S, {S → aS | B , B → b | bB })

G: ({S, A, B}, {a, b}, S, { S → aS | B , B → b | bB })

Example

Problem − 假设，L (G) = {am bn | m > 0 和 n ≥ 0}。我们必须找出生成 L(G) 的语法 G。

Problem − Suppose, L (G) = {am bn | m > 0 and n ≥ 0}. We have to find out the grammar G which produces L(G).

Solution −

因为 L(G) = {am bn | m > 0 和 n ≥ 0}，可接受的字符串集可重新写为 −

Since L(G) = {am bn | m > 0 and n ≥ 0}, the set of strings accepted can be rewritten as −

L(G) = {a, aa, ab, aaa, aab ,abb, …….}

此处，起始符号必须至少取一个“a”，后跟任意数量的“b”，包括零。

Here, the start symbol has to take at least one ‘a’ followed by any number of ‘b’ including null.

为接受字符串集 {a, aa, ab, aaa, aab, abb, …….}, 我们取了下面这些生成 −

To accept the string set {a, aa, ab, aaa, aab, abb, …….}, we have taken the productions −

S → aA, A → aA , A → B, B → bB ,B → λ

S → aA → aB → aλ → a （接受）

S → aA → aB → aλ → a (Accepted)

S → aA → aaA → aaB → aaλ → aa （接受）

S → aA → aaA → aaB → aaλ → aa (Accepted)

S → aA → aB → abB → abλ → ab （接受）

S → aA → aB → abB → abλ → ab (Accepted)

S → aA → aaA → aaaA → aaaB → aaaλ → aaa （接受）

S → aA → aaA → aaaA → aaaB → aaaλ → aaa (Accepted)

S → aA → aaA → aaB → aabB → aabλ → aab （接受）

S → aA → aaA → aaB → aabB → aabλ → aab (Accepted)

S → aA → aB → abB → abbB → abbλ → abb （接受）

S → aA → aB → abB → abbB → abbλ → abb (Accepted)

因此，我们可以证明 L(G) 中的每个字符串都由生成集合所生成的语义接受。

Thus, we can prove every single string in L(G) is accepted by the language generated by the production set.

因此语法 −

Hence the grammar −

G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB })

Chomsky Classification of Grammars

根据诺姆·乔姆斯基，语法有四种类型——第 0 类、第 1 类、第 2 类和第 3 类。下表显示了它们彼此之间的差异 -

According to Noam Chomosky, there are four types of grammars − Type 0, Type 1, Type 2, and Type 3. The following table shows how they differ from each other −

Grammar Type

Grammar Accepted

Language Accepted

Automaton

Type 0

Unrestricted grammar

Recursively enumerable language

Turing Machine

Type 1

Context-sensitive grammar

Context-sensitive language

Linear-bounded automaton

Type 2

Context-free grammar

Context-free language

Pushdown automaton

Type 3

Regular grammar

Regular language

Finite state automaton

看看以下插图。它显示了每种语法类型的范围 -

Take a look at the following illustration. It shows the scope of each type of grammar −

Type - 3 Grammar

q4 生成正则语言。Type-3 语法必须在左侧有一个非终结符，在右侧有一个终结符或一个终结符后跟一个非终结符。

Type-3 grammars generate regular languages. Type-3 grammars must have a single non-terminal on the left-hand side and a right-hand side consisting of a single terminal or single terminal followed by a single non-terminal.

产生式必须采用以下形式 Type-3 grammars

The productions must be in the form X → a or X → aY

其中 X → a or X → aY （非终结符）

where X, Y ∈ N (Non terminal)

和 X, Y ∈ N （终结符）

and a ∈ T (Terminal)

规则 a ∈ T 被允许，如果 S → ε 不出现在任何规则的右侧。

The rule S → ε is allowed if S does not appear on the right side of any rule.

Example

X → ε
X → a | aY
Y → b

Type - 2 Grammar

Type-2 grammars 生成上下文无关语言。

Type-2 grammars generate context-free languages.

产生式应为 A → γ 形式

The productions must be in the form A → γ

其中*A ∈ N*（非终结符）

where * A ∈ N* (Non terminal)

和 γ ∈ (T ∪ N) *（终结符和非终结符串）。

and γ ∈ (T ∪ N)* (String of terminals and non-terminals).

由这些语法生成的这些语言可被非确定性下推自动机识别。

These languages generated by these grammars are be recognized by a non-deterministic pushdown automaton.

Example

S → X a
X → a
X → aX
X → abc
X → ε

Type - 1 Grammar

Type-1 grammars 生成上下文相关语言。产生式应为

Type-1 grammars generate context-sensitive languages. The productions must be in the form

α A β → α γ β

其中 A ∈ N （非终结符）

where A ∈ N (Non-terminal)

和 α, β, γ ∈ (T ∪ N) *（终结符和非终结符串）。

and α, β, γ ∈ (T ∪ N)* (Strings of terminals and non-terminals)

字符串 α 和 β 可为空，但 γ 必须非空。

The strings α and β may be empty, but γ must be non-empty.

如果 S 未出现在任何规则的右侧，则规则 S → ε 是允许的。由这些语法生成的语言被线性有界自动机所识别。

The rule S → ε is allowed if S does not appear on the right side of any rule. The languages generated by these grammars are recognized by a linear bounded automaton.

Example

AB → AbBc
A → bcA
B → b

Type - 0 Grammar

Type-0 grammars 递归生成可枚举的语言。产生式没有任何限制。它们是包括所有形式文法的任意相结构语法。

Type-0 grammars generate recursively enumerable languages. The productions have no restrictions. They are any phase structure grammar including all formal grammars.

它们生成被图灵机识别的语言。

They generate the languages that are recognized by a Turing machine.

产生式可以 α → β 的形式出现，其中 α 是至少有一个非终结符的终结符和非终结符字符串，而 α 不能为 null。 β 是终结符和非终结符字符串。

The productions can be in the form of α → β where α is a string of terminals and nonterminals with at least one non-terminal and α cannot be null. β is a string of terminals and non-terminals.

Example

S → ACaB
Bc → acB
CB → DB
aD → Db

Regular Expressions

A Regular Expression 可按照以下方式递归定义 −

A Regular Expression can be recursively defined as follows −

ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
φ is a Regular Expression denoting an empty language. (L (φ) = { })
x is a Regular Expression where L = {x}
If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y). X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y) R is a Regular Expression corresponding to the language L(R)where *L(R) = (L®)*
If we apply any of the rules several times from 1 to 5, they are Regular Expressions.

Some RE Examples

Regular Expressions

Regular Set

(0 + 10*)

L = { 0, 1, 10, 100, 1000, 10000, … }

(0*10*)

L = {1, 01, 10, 010, 0010, …}

(0 + ε)(1 + ε)

L = {ε, 0, 1, 01}

(a+b)*

Set of strings of a’s and b’s of any length including the null string. So L = { ε, a, b, aa , ab , bb , ba, aaa…….}

(a+b)*abb

Set of strings of a’s and b’s ending with the string abb. So L = {abb, aabb, babb, aaabb, ababb, …………..}

(11)*

Set consisting of even number of 1’s including empty string, So L= {ε, 11, 1111, 111111, ……….}

(aa)*(bb)*b

Set of strings consisting of even number of a’s followed by odd number of b’s , so L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..}

(aa + ab + ba + bb)*

String of a’s and b’s of even length can be obtained by concatenating any combination of the strings aa, ab, ba and bb including null, so L = {aa, ab, ba, bb, aaab, aaba, …………..}

Regular Sets

任何表示正则表达式值的集合都被称为 Regular Set.

Any set that represents the value of the Regular Expression is called a Regular Set.

Properties of Regular Sets

Property 1 . 两个正则集的并集是正则。

Property 1. The union of two regular set is regular.

Proof −

让我们取两个正则表达式

Let us take two regular expressions

RE1 = a(aa)，RE2 = (aa)

RE1 = a(aa)* and RE2 = (aa)*

所以，L1 = {a, aaa, aaaaa,…..}（不包括 Null 的奇数长度字符串）

So, L1 = {a, aaa, aaaaa,…..} (Strings of odd length excluding Null)

且 L2 ={ ε, aa, aaaa, aaaaaa,…….} （包括 Null 的偶数长度字符串）

and L2 ={ ε, aa, aaaa, aaaaaa,…….} (Strings of even length including Null)

L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,…….}

（包括 Null 的所有可能长度的字符串）

(Strings of all possible lengths including Null)

RE (L1 ∪ L2) = a* （本身就是一个正则表达式）

RE (L1 ∪ L2) = a* (which is a regular expression itself)

Hence, proved.

Property 2. 两个正则集的交集是正则。

Property 2. The intersection of two regular set is regular.

Proof −

让我们取两个正则表达式

Let us take two regular expressions

RE1 = a(a*)，RE2 = (aa)*

RE1 = a(a*) and RE2 = (aa)*

所以，L1 = { a,aa, aaa, aaaa, ….} （不包括 Null 的所有可能长度字符串）

So, L1 = { a,aa, aaa, aaaa, ….} (Strings of all possible lengths excluding Null)

L2 = { ε, aa, aaaa, aaaaaa,…}（包含空字符串的偶数长度字符串）

L2 = { ε, aa, aaaa, aaaaaa,…….} (Strings of even length including Null)

L1 ∩ L2 = { aa, aaaa, aaaaaa,…}（不包含空字符串的偶数长度字符串）

L1 ∩ L2 = { aa, aaaa, aaaaaa,…….} (Strings of even length excluding Null)

RE (L1 ∩ L2) = aa(aa)*，本身是一个正则表达式。

RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.

Hence, proved.

Property 3. 一个正则集合的补集是正则的。

Property 3. The complement of a regular set is regular.

Proof −

我们取正则表达式−

Let us take a regular expression −

RE = (aa)*

所以，L = {ε, aa, aaaa, aaaaaa, …}（包含空字符串的偶数长度字符串）

So, L = {ε, aa, aaaa, aaaaaa, …….} (Strings of even length including Null)

L 的补集是不在 L 中的所有字符串。

Complement of L is all the strings that is not in L.

所以，L’ = {a, aaa, aaaaa, …}（不包含空字符串的奇数长度字符串）

So, L’ = {a, aaa, aaaaa, …..} (Strings of odd length excluding Null)

RE (L’) = a(aa)*，本身是一个正则表达式。

RE (L’) = a(aa)* which is a regular expression itself.

Hence, proved.

Property 4. 两个正则集合的差是正则的。

Property 4. The difference of two regular set is regular.

Proof −

我们取两个正则表达式−

Let us take two regular expressions −

RE1 = a (a*) 和 RE2 = (aa)*

RE1 = a (a*) and RE2 = (aa)*

所以，L1 = {a, aa, aaa, aaaa, …}（包含所有可能的长度且不包含空字符串的字符串）

So, L1 = {a, aa, aaa, aaaa, ….} (Strings of all possible lengths excluding Null)

L2 = { ε, aa, aaaa, aaaaaa,…}（包含空字符串的偶数长度字符串）

L2 = { ε, aa, aaaa, aaaaaa,…….} (Strings of even length including Null)

L1 – L2 = {a, aaa, aaaaa, aaaaaaa, …}

L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ….}

（不包含空字符串的所有奇数长度字符串）

(Strings of all odd lengths excluding Null)

RE (L1 – L2) = a (aa)*，是一个正则表达式。

RE (L1 – L2) = a (aa)* which is a regular expression.

Hence, proved.

Property 5. 一个正则集合的反转是正则的。

Property 5. The reversal of a regular set is regular.

Proof −

我们要证明 LR 也是正则的，如果 L 是一个正则集合。

We have to prove LR is also regular if L is a regular set.

令 L = {01，10，11，10}

Let, L = {01, 10, 11, 10}

RE (L) = 01 + 10 + 11 + 10

LR = {10，01，11，01}

LR = {10, 01, 11, 01}

RE (LR) = 01 + 10 + 11 + 10 为正则语言

RE (LR) = 01 + 10 + 11 + 10 which is regular

Hence, proved.

Property 6. 正则集合的闭包为正则语言。

Property 6. The closure of a regular set is regular.

Proof −

如果 L = {a, aaa, aaaaa, …….} （长度为奇数且不含空集合的字符串），

If L = {a, aaa, aaaaa, …….} (Strings of odd length excluding Null)

即 RE (L) = a (aa)*

i.e., RE (L) = a (aa)*

L* = {a, aa, aaa, aaaa , aaaaa,……………} （长度可为任意正整数且不含空集合的字符串）

L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)

RE (L*) = a (a)*

Hence, proved.

Property 7. 两个正则集合的连接为正则语言。

Property 7. The concatenation of two regular sets is regular.

Proof −

令 RE1 = (0+1) 0 and RE2 = 01(0+1)

Let RE1 = (0+1)0 and RE2 = 01(0+1)

此处，L1 = {0, 00, 10, 000, 010, ……} （以 0 结尾的字符串集合）

Here, L1 = {0, 00, 10, 000, 010, ……} (Set of strings ending in 0)

且 L2 = {01, 010,011,…..} （以 01 开头的字符串集合）

and L2 = {01, 010,011,…..} (Set of strings beginning with 01)

则 L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,………….}

Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,………….}

包含 001 作为子串的字符串集合，可以用正则表达式表示为 − (0 + 1) 001(0 + 1)

Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)001(0 + 1)

因此得证。

Hence, proved.

Identities Related to Regular Expressions

给出正则表达式 R, P, L, Q，则有如下恒等式：

Given R, P, L, Q as regular expressions, the following identities hold −

∅* = ε
ε* = ε
RR* = R*R
R*R* = R*
(R*)* = R*
RR* = R*R
(PQ)P =P(QP)
(a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
R + ∅ = ∅ + R = R (The identity for union)
R ε = ε R = R (The identity for concatenation)
∅ L = L ∅ = ∅ (The annihilator for concatenation)
R + R = R (Idempotent law)
L (M + N) = LM + LN (Left distributive law)
(M + N) L = ML + NL (Right distributive law)
ε + RR* = ε + R*R = R*

Arden’s Theorem

为了找出有限自动机的正则表达式，我们使用 Arden 定理以及正则表达式的性质。

In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.

Statement -

Statement −

设 P 和 Q 是两个正则表达式。

Let P and Q be two regular expressions.

如果 P 不包含 null 字符串，则 R = Q + RP 具有唯一解 R = QP *

If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*

Proof −

R = Q + (Q + RP)P [在代入了 R = Q + RP 之后]

R = Q + (Q + RP)P [After putting the value R = Q + RP]

Q + QP + RPP

当我们不断递归地代入 R 的值时，我们得到以下方程 -

When we put the value of R recursively again and again, we get the following equation −

R = Q + QP + QP2 + QP3…..

R = Q (ε + P + P2 + P3 + …. )

R = QP* [因为 P* 表示 (ε + P + P2 + P3 + ….) ]

R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]

因此得证。

Hence, proved.

Assumptions for Applying Arden’s Theorem

The transition diagram must not have NULL transitions
It must have only one initial state

Method

Step 1 - 对于所有具有 n 个状态的 DFA 状态（初始状态为 q1），创建以下形式的方程。

Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.

q1 = q1R11 + q2R21 + … + qnRn1 + ε

q2 = q1R12 + q2R22 + … + qnRn2

…………………………

qn = q1R1n + q2R2n + … + qnRnn

Rij 表示从 qi 到 qj 的边的标签集合，如果不存在这样的边，则 Rij = ∅

Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅

Step 2 — 求解这些方程式，以 Rij 的形式获得最终状态方程式

Step 2 − Solve these equations to get the equation for the final state in terms of Rij

Problem

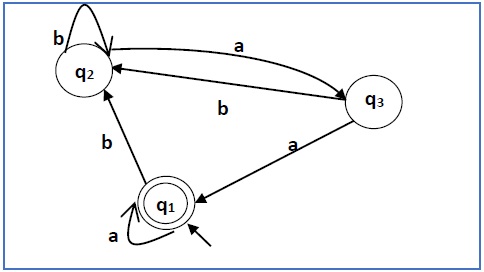
构造与以下给定自动机相对应的正则表达式 −

Construct a regular expression corresponding to the automata given below −

Solution −

此处初始状态和最终状态为 q1 。

Here the initial state and final state is q1.

三个状态 q1、q2 和 q3 的方程式如下 −

The equations for the three states q1, q2, and q3 are as follows −

q1 = q1a + q3a + ε（ε 移动是因为 q1 是初始状态 0

q1 = q1a + q3a + ε (ε move is because q1 is the initial state0

q2 = q1b + q2b + q3b

q3 = q2a

现在，我们将求解这三个方程式 −

Now, we will solve these three equations −

q2 = q1b + q2b + q3b

q1b + q2b + (q2a)b (Substituting value of q3)

q1b + q2(b + ab)

q1b (b + ab)* (Applying Arden’s Theorem)

q1 = q1a + q3a + ε

q1a + q2aa + ε (Substituting value of q3)

q1a + q1b(b + ab*)aa + ε (Substituting value of q2)

q1(a + b(b + ab)*aa) + ε

ε (a+ b(b + ab)aa)

(a + b(b + ab)aa)

因此，正则表达式为 (a + b(b + ab) aa) 。

Hence, the regular expression is (a + b(b + ab)aa).

Problem

构造与以下给定自动机相对应的正则表达式 −

Construct a regular expression corresponding to the automata given below −

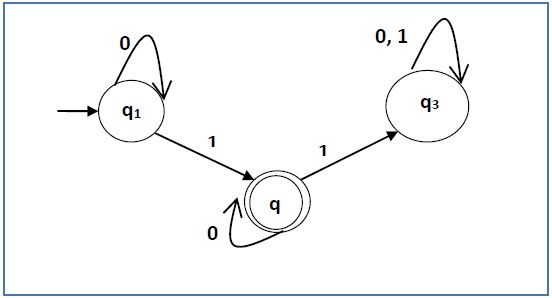
Solution −

此处初始状态为 q1，最终状态为 q2

Here the initial state is q1 and the final state is q2

现在我们写下方程式 −

Now we write down the equations −

q1 = q10 + ε

q2 = q11 + q20

q3 = q21 + q30 + q31

现在，我们将求解这三个方程式 −

Now, we will solve these three equations −

q1 = ε0* [，εR = R]

q1 = ε0* [As, εR = R]

所以，q1 = 0*

So, q1 = 0*

q2 = 0*1 + q20

所以，q2 = 0*1(0)* [由艾登定理]

So, q2 = 0*1(0)* [By Arden’s theorem]

因此，正则表达式为 0*10*。

Hence, the regular expression is 0*10*.

Construction of an FA from an RE

我们可以使用汤普森构建法发现一个由正则表达式构造的有穷自动机。我们将正则表达式简化为最小的正则表达式，然后将这些表达式转换为 NFA，最后转换为 DFA。

We can use Thompson’s Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.

一些基本的 RA 表达式为：

Some basic RA expressions are the following −

Case 1 －对于正则表达式“a”，我们可以构造以下 FA －

Case 1 − For a regular expression ‘a’, we can construct the following FA −

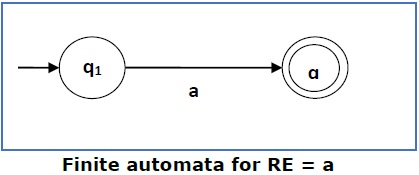
Case 2 − 对于正则表达式“ab”，我们可以构建以下 FA −

Case 2 − For a regular expression ‘ab’, we can construct the following FA −

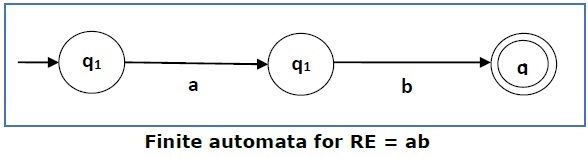
Case 3 − 对于正则表达式 (a+b)，我们可以构建以下 FA −

Case 3 − For a regular expression (a+b), we can construct the following FA −

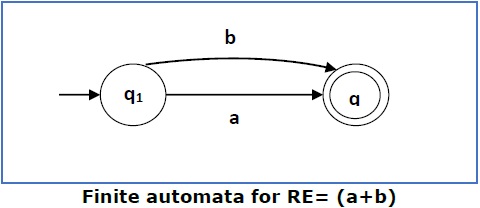
Case 4 − 对于正则表达式 (a+b)*，我们可以构建以下 FA −

Case 4 − For a regular expression (a+b)*, we can construct the following FA −

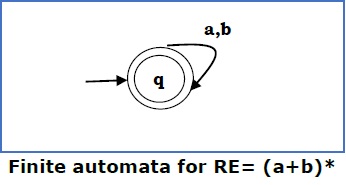
Method

Step 1 根据给定的正则表达式构建一个带有空动作的 NFA。

Step 1 Construct an NFA with Null moves from the given regular expression.

Step 2 从 NFA 中删除空转换，并将其转换成等效的 DFA。

Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.

Problem

将以下 RA 转换成等效的 DFA − 1 (0 + 1)* 0

Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0

Solution

我们将三个表达式“1”、“(0 + 1)*”和“0”连接在一起

We will concatenate three expressions "1", "(0 + 1)*" and "0"

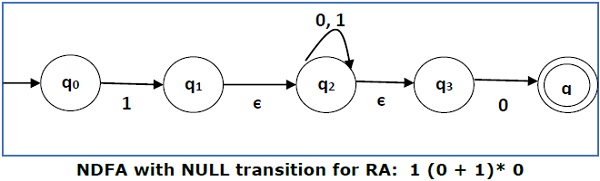
现在我们将删除 ε 转换。从 NDFA 中删除 ε 转换后，我们得到以下结果 −

Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

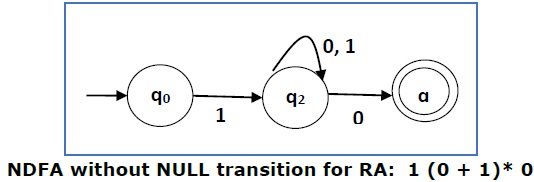
它是与 RE − 1 (0 + 1)* 0 相对应的 NDFA。如果你想将其转换成 DFA，只需应用第 1 章中讨论的 NDFA 到 DFA 的转换方法。

It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.

Finite Automata with Null Moves (NFA-ε)

带有空动作的有限自动机 (FA-ε) 不仅在从字母集合提供输入后进行转换，还可以在没有输入符号的情况下进行转换。这种没有输入的转换称为 null move 。

A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.

NFA-ε 由一个 5 元组（Q、∑、δ、q0、F）正式表示，其中包括

An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of

Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).

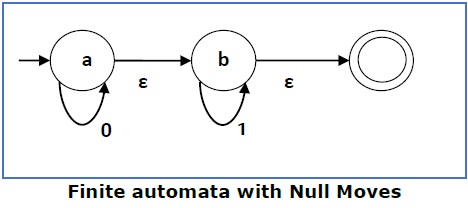
上述 (FA-ε) 接受一个字符串集合 − {0, 1, 01}

The above (FA-ε) accepts a string set − {0, 1, 01}

Removal of Null Moves from Finite Automata

如果在 NDFA 中，存在从顶点 X 到顶点 Y 的 ϵ 动作，我们可以使用以下步骤将其删除 −

If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −

Find all the outgoing edges from Y.
Copy all these edges starting from X without changing the edge labels.
If X is an initial state, make Y also an initial state.
If Y is a final state, make X also a final state.

Problem

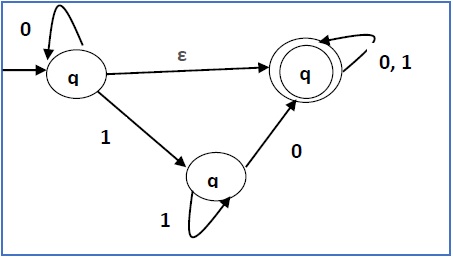
将以下 NFA-ε 转换为没有空移动的 NFA。

Convert the following NFA-ε to NFA without Null move.

Solution

Step 1 -

Step 1 −

这里 ε 转换在 q1 和 q2 之间，所以让 q1 等于 X ，而 qf 等于 Y 。

Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.

这里从 qf 出发到 qf 的输出边针对输入 0 和 1。

Here the outgoing edges from qf is to qf for inputs 0 and 1.

Step 2 -

Step 2 −

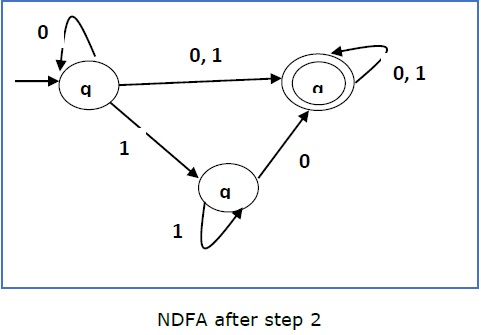
现在，我们将从 q1 复制所有这些边，而不会更改从 qf 分出的边，并获得以下 FA −

Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −

Step 3 -

Step 3 −

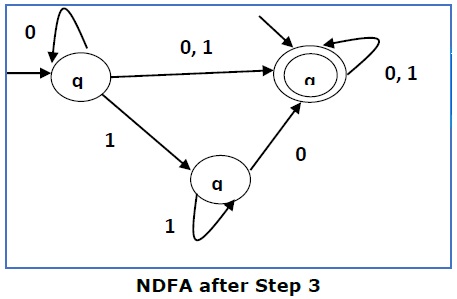
这里 q1 是一个初始状态，所以我们也将 qf 设置为初始状态。

Here q1 is an initial state, so we make qf also an initial state.

因此 FA 变成 −

So the FA becomes −

Step 4 -

Step 4 −

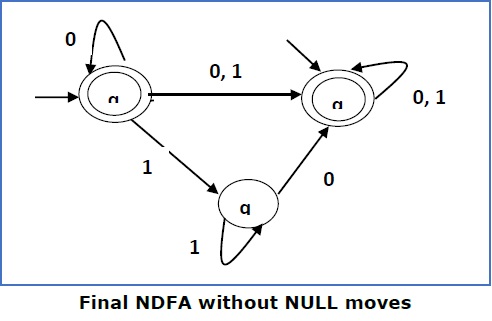
这里 qf 是一个终止状态，因此我们也将 q1 设置为终止状态。

Here qf is a final state, so we make q1 also a final state.

因此 FA 变成 −

So the FA becomes −

Pumping Lemma For Regular Grammars

Theorem

设 L 是正则语言。那么存在常量 ‘c’ 使得对于 L 中的每个字符串 w −

Let L be a regular language. Then there exists a constant ‘c’ such that for every string w in L −

|w| ≥ c

我们可以把 w 分成三个字符串 w = xyz ，使得 −

We can break w into three strings, w = xyz, such that −

|y| > 0
|xy| ≤ c
For all k ≥ 0, the string xykz is also in L.

Applications of Pumping Lemma

抽取引理用于证明某些语言不是正则的。它不应该被用来证明语言是正则的。

Pumping Lemma is to be applied to show that certain languages are not regular. It should never be used to show a language is regular.

If L is regular, it satisfies Pumping Lemma.
If L does not satisfy Pumping Lemma, it is non-regular.

Method to prove that a language L is not regular

At first, we have to assume that L is regular.
So, the pumping lemma should hold for L.
Use the pumping lemma to obtain a contradiction − Select w such that |w| ≥ c Select y such that |y| ≥ 1 Select x such that |xy| ≤ c Assign the remaining string to z. Select k such that the resulting string is not in L.

Hence L is not regular.

Problem

证明 L = {aibi | i ≥ 0} 不是正则的。

Prove that L = {aibi | i ≥ 0} is not regular.

Solution −

At first, we assume that L is regular and n is the number of states.
Let w = anbn. Thus |w| = 2n ≥ n.
By pumping lemma, let w = xyz, where |xy| ≤ n.
Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
Let k = 2. Then xy2z = apa2qarbn.
Number of as = (p + 2q + r) = (p + q + r) + q = n + q
Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
Thus, xy2z is not in L. Hence L is not regular.

DFA Complement

如果 (Q, ∑, δ, q0, F) 是接受语言 L 的 DFA，则可以通过将接受状态与非接受状态以及反之互换来获得 DFA 的补集。

If (Q, ∑, δ, q0, F) be a DFA that accepts a language L, then the complement of the DFA can be obtained by swapping its accepting states with its non-accepting states and vice versa.

我们将举例并在下面详细说明 −

We will take an example and elaborate this below −

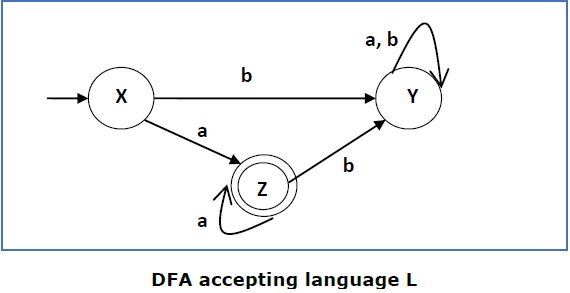
此 DFA 接受语言

This DFA accepts the language

L = {a, aa, aaa , …………. }

在字母表上

over the alphabet

∑ = {a, b}

所以，RE = a+。

So, RE = a+.

现在，我们将它的接受状态与其不接受状态互换，反之亦然，并且将获得以下状态：

Now we will swap its accepting states with its non-accepting states and vice versa and will get the following −

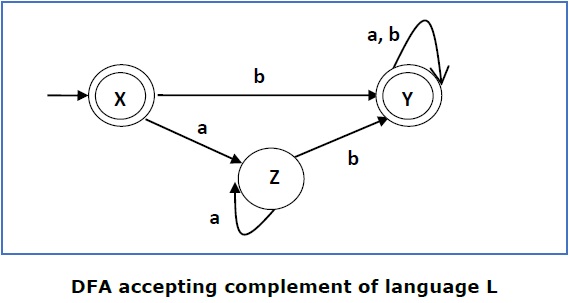
此 DFA 接受语言

This DFA accepts the language

Ľ = {ε, b, ab、bb、ba、…………… }

Ľ = {ε, b, ab ,bb,ba, …………… }

在字母表上

over the alphabet

∑ = {a, b}

Note - 如果我们希望对 NFA 求补，我们必须首先将其转换为 DFA，然后像在前面的方法中一样交换状态。

Note − If we want to complement an NFA, we have to first convert it to DFA and then have to swap states as in the previous method.

Context-Free Grammar Introduction

Definition - 上下文无关文法 (CFG) 由一组有限的文法规则组成，是四元组 (N, T, P, S) ，其中

Definition − A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where

N is a set of non-terminal symbols.
T is a set of terminals where N ∩ T = NULL.
P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
S is the start symbol.

Example

The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε

Generation of Derivation Tree

导出树或解析树是有序的根树，可以直观地表示从上下文无关文法导出的字符串的语义信息。

A derivation tree or parse tree is an ordered rooted tree that graphically represents the semantic information a string derived from a context-free grammar.

Representation Technique

Root vertex − Must be labeled by the start symbol.
Vertex − Labeled by a non-terminal symbol.
Leaves − Labeled by a terminal symbol or ε.

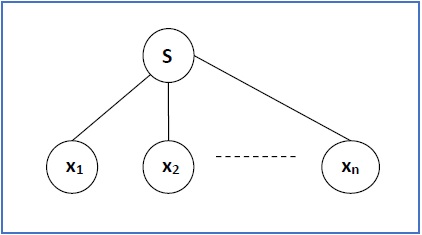
如果 S → x1x2 …… xn 是 CFG 中的一条产生规则，则解析树/导出树如下：

If S → x1x2 …… xn is a production rule in a CFG, then the parse tree / derivation tree will be as follows −

绘制导出树有两种不同的方法：

There are two different approaches to draw a derivation tree −

Top-down Approach −

Starts with the starting symbol S
Goes down to tree leaves using productions

Bottom-up Approach −

Starts from tree leaves
Proceeds upward to the root which is the starting symbol S

Derivation or Yield of a Tree

解析树的导出或产生的最终字符串通过从左到右串联树的叶子的标签获得，而忽略空值。然而，如果所有叶子都是空值，那么派生就是空值。

The derivation or the yield of a parse tree is the final string obtained by concatenating the labels of the leaves of the tree from left to right, ignoring the Nulls. However, if all the leaves are Null, derivation is Null.

Example

令 CFG 为 {N,T,P,S}

Let a CFG {N,T,P,S} be

N = {S}, T = {a, b}, 开始符号 = S, P = S → SS | aSb | ε

N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | ε

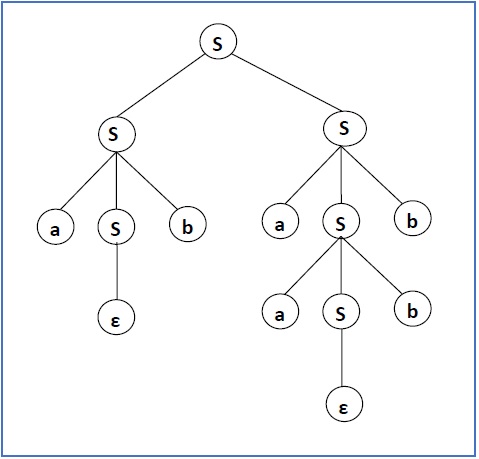
上述 CFG 的一个派生是“abaabb”

One derivation from the above CFG is “abaabb”

S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Sentential Form and Partial Derivation Tree

部分派生树是派生树/解析树的一个子树，使得它的所有子组件都在子树中，或者它们都不在子树中。

A partial derivation tree is a sub-tree of a derivation tree/parse tree such that either all of its children are in the sub-tree or none of them are in the sub-tree.

Example

在任何 CFG 中，如果生成是 -

If in any CFG the productions are −

S → AB, A → aaA | ε, B → Bb| ε

部分派生树可以是以下 -

the partial derivation tree can be the following −

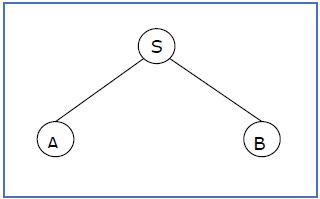
sentential form and partial derivation tree

如果部分派生树包含根 S，则称为 sentential form 。上述子树也是以句子形式出现的。

If a partial derivation tree contains the root S, it is called a sentential form. The above sub-tree is also in sentential form.

Leftmost and Rightmost Derivation of a String

Leftmost derivation − A leftmost derivation is obtained by applying production to the leftmost variable in each step.
Rightmost derivation − A rightmost derivation is obtained by applying production to the rightmost variable in each step.

Example

设 CFG 中的任何一组生成规则

Let any set of production rules in a CFG be

X → X+X | X*X |X| a

在一个字母表 {a} 中。

over an alphabet {a}.

字符串 "a+a*a" 最左侧推导可能如下 −

The leftmost derivation for the string "a+a*a" may be −

X → X+X → a+X → a + X*X → a+a*X → a+a*a

以上字符串逐步推导如下 −

The stepwise derivation of the above string is shown as below −

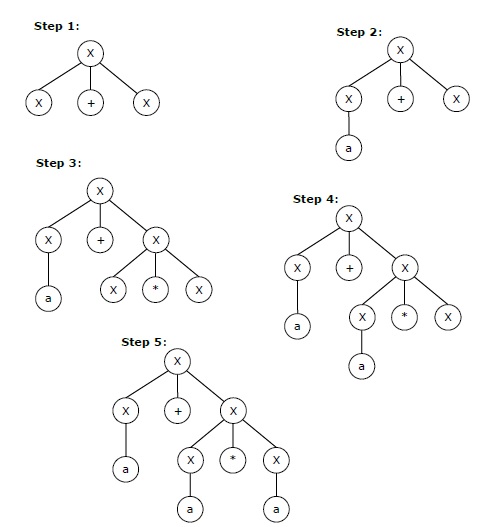
字符串 "a+a*a" 最右侧推导可能如下 −

The rightmost derivation for the above string "a+a*a" may be −

X → X*X → X*a → X+X*a → X+a*a → a+a*a

以上字符串逐步推导如下 −

The stepwise derivation of the above string is shown as below −

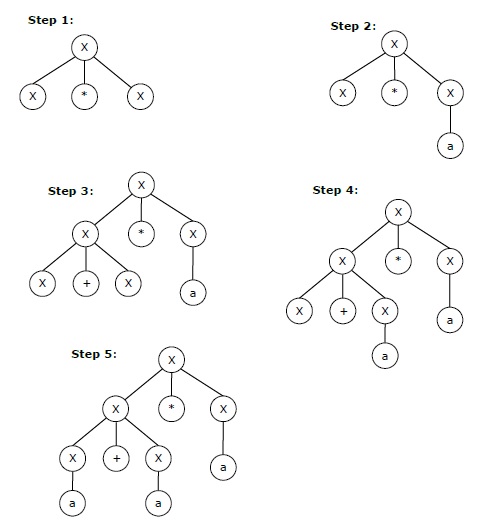
Left and Right Recursive Grammars

在一个上下文无关文法中 G ，如果有一个形式为 X → Xa 的产生式，其中 X 是一个非终结符， ‘a’ 是一个终结符字符串，它被称为 left recursive production 。具有左递归产生式的文法称为 left recursive grammar 。

In a context-free grammar G, if there is a production in the form X → Xa where X is a non-terminal and ‘a’ is a string of terminals, it is called a left recursive production. The grammar having a left recursive production is called a left recursive grammar.

而如果在一个上下文无关文法中 G ，如果有一个形式为 X → aX 的产生式，其中 X 是一个非终结符， ‘a’ 是一个终结符字符串，它被称为 right recursive production 。具有右递归产生式的文法称为 right recursive grammar 。

And if in a context-free grammar G, if there is a production is in the form X → aX where X is a non-terminal and ‘a’ is a string of terminals, it is called a right recursive production. The grammar having a right recursive production is called a right recursive grammar.

Ambiguity in Context-Free Grammars

如果某个无上下文文法 G 对于某个字符串 w ∈ L(G) 有多个派生树，则称其为 ambiguous grammar 。从该文法生成的某个字符串存在多个最右或最左派生。

If a context free grammar G has more than one derivation tree for some string w ∈ L(G), it is called an ambiguous grammar. There exist multiple right-most or left-most derivations for some string generated from that grammar.

Problem

检查产生规则为 −

Check whether the grammar G with production rules −

X → X+X | X*X |X| a

的文法 G 是否模糊。

is ambiguous or not.

Solution

让我们找出字符串“a+a*a”的派生树。它有两个最左派生。

Let’s find out the derivation tree for the string "a+a*a". It has two leftmost derivations.

Derivation 1 −X → X+X → a X → a X*X → a+a*X → a+a*a

Derivation 1 − X → X+X → a X → a X*X → a+a*X → a+a*a

Parse tree 1 −

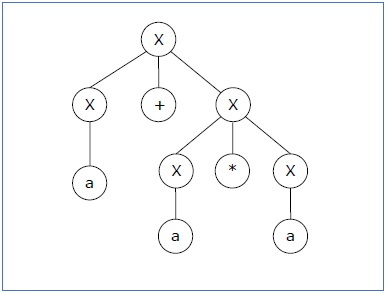
Derivation 2 − X → X*X → X+X*X → a+ X*X → a+a*X → a+a*a

Parse tree 2 −

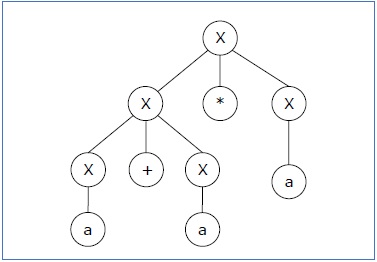
由于对于单个字符串“a+a*a”有两个解析树，文法 G 是模糊的。

Since there are two parse trees for a single string "a+a*a", the grammar G is ambiguous.

CFL Closure Property

无上下文语言在 − 下为 closed

Context-free languages are closed under −

Union
Concatenation
Kleene Star operation

Union

设 L1 和 L2 为两种无上下文语言。则 L1 ∪ L2 也是无上下文的。

Let L1 and L2 be two context free languages. Then L1 ∪ L2 is also context free.

Example

设 L1 = { anbn , n > 0}。相应的语法 G1 具有 P: S1 → aAb|ab

Let L1 = { anbn , n > 0}. Corresponding grammar G1 will have P: S1 → aAb|ab

设 L2 = { cmdm , m ≥ 0}。相应的语法 G2 具有 P: S2 → cBb| ε

Let L2 = { cmdm , m ≥ 0}. Corresponding grammar G2 will have P: S2 → cBb| ε

L1 和 L2 的并集，L = L1 ∪ L2 = { anbn } ∪ { cmdm }

Union of L1 and L2, L = L1 ∪ L2 = { anbn } ∪ { cmdm }

相应的语法 G 将具有附加产生式 S → S1 | S2

The corresponding grammar G will have the additional production S → S1 | S2

Concatenation

如果 L1 和 L2 是无上下文语言，则 L1L2 也是无上下文的。

If L1 and L2 are context free languages, then L1L2 is also context free.

Example

语言 L1 和 L2 的并集，L = L1L2 = { anbncmdm }

Union of the languages L1 and L2, L = L1L2 = { anbncmdm }

相应的语法 G 将具有附加产生式 S → S1 S2

The corresponding grammar G will have the additional production S → S1 S2

Kleene Star

若 L 是上下文无关语言，那么 L* 也是上下文无关语言。

If L is a context free language, then L* is also context free.

Example

设 L = { anbn ，n ≥ 0}。对应的文法 G 将具有 P: S → aAb| ε

Let L = { anbn , n ≥ 0}. Corresponding grammar G will have P: S → aAb| ε

Kleene 星号 L1 = { anbn }*

Kleene Star L1 = { anbn }*

对应的文法 G1 将具有附加产生式 S1 → SS1 | ε

The corresponding grammar G1 will have additional productions S1 → SS1 | ε

上下文无关语言在 − 下属于 not closed

Context-free languages are not closed under −

Intersection − If L1 and L2 are context free languages, then L1 ∩ L2 is not necessarily context free.
Intersection with Regular Language − If L1 is a regular language and L2 is a context free language, then L1 ∩ L2 is a context free language.
Complement − If L1 is a context free language, then L1’ may not be context free.

CFG Simplification

在一个 CFG 中，所有产生式和符号可能不一定都用于推导字符串。此外，可能存在一些空产生式和单位产生式。消除这些产生式和符号被称为 simplification of CFGs 。简化主要包括以下步骤 −

In a CFG, it may happen that all the production rules and symbols are not needed for the derivation of strings. Besides, there may be some null productions and unit productions. Elimination of these productions and symbols is called simplification of CFGs. Simplification essentially comprises of the following steps −

Reduction of CFG
Removal of Unit Productions
Removal of Null Productions

Reduction of CFG

CFG 分为两个阶段来简化 −

CFGs are reduced in two phases −

Phase 1 − 从 CFG G 推导出一个等价文法 G’ ，使得每个变量都推导出某个终结符字符串。

Phase 1 − Derivation of an equivalent grammar, G’, from the CFG, G, such that each variable derives some terminal string.

Derivation Procedure −

步骤 1 − 包含所有推导出某个终结符的符号 W1 ，并初始化 i=1 。

Step 1 − Include all symbols, W1, that derive some terminal and initialize i=1.

步骤 2 − 包含所有推导出 Wi 的符号 Wi+1 。

Step 2 − Include all symbols, Wi+1, that derive Wi.

步骤 3 − 增加 i 并重复步骤 2，直到 Wi+1 = Wi 。

Step 3 − Increment i and repeat Step 2, until Wi+1 = Wi.

步骤 4 − 包含所有包含 Wi 的产生式。

Step 4 − Include all production rules that have Wi in it.

Phase 2 − 从 CFG G’ 推导出一个等价文法 G” ，使得每个符号都出现在句式中。

Phase 2 − Derivation of an equivalent grammar, G”, from the CFG, G’, such that each symbol appears in a sentential form.

Derivation Procedure −

步骤 1 − 将起始符号包含在 Y1 中，并初始化 i = 1 。

Step 1 − Include the start symbol in Y1 and initialize i = 1.

步骤 2 − 包含所有可以从 Yi 推导出的符号 Yi+1 ，并包含所有已经应用的产生式。

Step 2 − Include all symbols, Yi+1, that can be derived from Yi and include all production rules that have been applied.

步骤 3 − 增加 i 并重复步骤 2，直到 Yi+1 = Yi 。

Step 3 − Increment i and repeat Step 2, until Yi+1 = Yi.

Problem

找到与语法 G 等价的简化语法，其中产生式为 P：S → AC | B，A → a，C → c | BC，E → aA | e

Find a reduced grammar equivalent to the grammar G, having production rules, P: S → AC | B, A → a, C → c | BC, E → aA | e

Solution

Phase 1 −

T = {a, c, e}

T = { a, c, e }

根据产生式 A → a, C → c 和 E →aAa，W1 = {A, C, E}

W1 = { A, C, E } from rules A → a, C → c and E → aA

根据产生式 S → AC，W2 = { A, C, E } U { S }

W2 = { A, C, E } U { S } from rule S → AC

W3 = {A, C, E, S} U ∅

W3 = { A, C, E, S } U ∅

由于 W2 = W3，我们可以推导出 G' 为：

Since W2 = W3, we can derive G’ as −

G' = {{A, C, E, S}, {a, c, e}, P, {S}}

G’ = { { A, C, E, S }, { a, c, e }, P, {S}}

其中 P：S → AC，A → a，C → c，E → aA | e

where P: S → AC, A → a, C → c , E → aA | e

Phase 2 −

根据产生式 S → AC，Y1 = {S}

Y1 = { S }

Y2 = {S, A, C}

Y2 = { S, A, C } from rule S → AC

根据产生式 A → a 和 C → c，Y3 = {S, A, C, a, c}

Y3 = { S, A, C, a, c } from rules A → a and C → c

Y4 = {S, A, C, a, c}

Y4 = { S, A, C, a, c }

由于 Y3 = Y4，我们可以推导出 G'' 为：

Since Y3 = Y4, we can derive G” as −

G'' = {{A, C, S}, {a, c}, P, {S}}

G” = { { A, C, S }, { a, c }, P, {S}}

其中 P：S → AC，A → a，C → c

where P: S → AC, A → a, C → c

Removal of Unit Productions

任何形式为 A → B 的产生式，其中 A, B ∈ 非终结符被称作 unit production. 。

Any production rule in the form A → B where A, B ∈ Non-terminal is called unit production..

Removal Procedure −

Step 1 − 要消除 A → B ，只要在语法中出现 B → x 时，就添加到语法规则中产生式 A → x 。[x ∈ 终结符，x 可以为空]

Step 1 − To remove A → B, add production A → x to the grammar rule whenever B → x occurs in the grammar. [x ∈ Terminal, x can be Null]

Step 2 ——从语法中删除 A → B 。

Step 2 − Delete A → B from the grammar.

Step 3 ——从步骤 1 开始重复，直到删除所有单位产生式。

Step 3 − Repeat from step 1 until all unit productions are removed.

Problem

从以下内容中删除单位产生式 -.

Remove unit production from the following −

S → XY、X → a、Y → Z | b、Z → M、M → N、N → a

S → XY, X → a, Y → Z | b, Z → M, M → N, N → a

Solution −

语法中有 3 个单位产生式-

There are 3 unit productions in the grammar −

Y → Z、Z → M和 M → N

Y → Z, Z → M, and M → N

At first, we will remove M → N.

由于 N → a，我们添加 M → a，并删除 M → N。

As N → a, we add M → a, and M → N is removed.

产生式集变为

The production set becomes

S → XY、X → a、Y → Z | b、Z → M、M → a、N → a

S → XY, X → a, Y → Z | b, Z → M, M → a, N → a

Now we will remove Z → M.

由于 M → a，我们添加 Z→ a，并删除 Z → M。

As M → a, we add Z→ a, and Z → M is removed.

产生式集变为

The production set becomes

S → XY、X → a、Y → Z | b、Z → a、M → a、N → a

S → XY, X → a, Y → Z | b, Z → a, M → a, N → a

Now we will remove Y → Z.

由于 Z → a，我们添加 Y→ a，并删除 Y → Z。

As Z → a, we add Y→ a, and Y → Z is removed.

产生式集变为

The production set becomes

S → XY、X → a、Y → a | b、Z → a、M → a、N → a

S → XY, X → a, Y → a | b, Z → a, M → a, N → a

现在 Z、M和 N 不可达，因此我们可以删除它们。

Now Z, M, and N are unreachable, hence we can remove those.

最终的 CFG 没有单位产生式 -.

The final CFG is unit production free −

S → XY、X → a、Y → a | b

S → XY, X → a, Y → a | b

Removal of Null Productions

在 CFG 中，非终结符 ‘A’ 是一个空值变量，如果存在产生式 A → ε 或存在从 A 开始最终以

In a CFG, a non-terminal symbol ‘A’ is a nullable variable if there is a production A → ε or there is a derivation that starts at A and finally ends up with

ε: A → …….… → ε

Removal Procedure

Step 1 结束的推导 - 找出导出 ε 的空值非终结符变量。

Step 1 − Find out nullable non-terminal variables which derive ε.

Step 2 - 对于每个产生式 A → a ，构建所有产生式 A → x ，其中 x 是通过从步骤 1 中移除一个或多个非终结符从 ‘a’ 获得的。

Step 2 − For each production A → a, construct all productions A → x where x is obtained from ‘a’ by removing one or multiple non-terminals from Step 1.

Step 3 - 将原始产生式与步骤 2 的结果合并，并移除 ε - productions 。

Step 3 − Combine the original productions with the result of step 2 and remove ε - productions.

Problem

从以下内容中移除空值产生式 -

Remove null production from the following −

S → ASA | aB | b, A → B, B → b | ∈

Solution −

有两个空值变量 - A 和 B

There are two nullable variables − A and B

At first, we will remove B → ε.

移除 B → ε 后，产生式集变为 -

After removing B → ε, the production set becomes −

S→ASA | aB | b | a，A ε B| b | &epsilon，B → b

S→ASA | aB | b | a, A ε B| b | &epsilon, B → b

Now we will remove A → ε.

去掉 A → ε 后，产生式集变为−

After removing A → ε, the production set becomes −

S→ASA | aB | b | a | SA | AS | S，A → B| b，B → b

S→ASA | aB | b | a | SA | AS | S, A → B| b, B → b

这是去除空串转换的最终产生式集。

This is the final production set without null transition.

Chomsky Normal Form

如果产生式满足以下形式，则一个 CFG 处于乔姆斯基范式−

A CFG is in Chomsky Normal Form if the Productions are in the following forms −

A → a
A → BC
S → ε

其中 A、B 和 C 是非终结符，而 a 是终结符。

where A, B, and C are non-terminals and a is terminal.

Algorithm to Convert into Chomsky Normal Form −

Step 1 − 如果起始符号 S 出现在某个右侧，创建一个新的起始符号 S’ 和一个新的产生式 S’→ S 。

Step 1 − If the start symbol S occurs on some right side, create a new start symbol S’ and a new production S’→ S.

Step 2 − 删除空产生式。（使用前面讨论的空产生式消除算法）

Step 2 − Remove Null productions. (Using the Null production removal algorithm discussed earlier)

Step 3 − 删除单位产生式。（使用前面讨论的单位产生式消除算法）

Step 3 − Remove unit productions. (Using the Unit production removal algorithm discussed earlier)

Step 4 − 替换每个将 n > 2 替换成 A → B1C 产生的 A → B1…Bn ，将 C → B2 …Bn 替换成 A → B1C 。对右侧有两个或更多符号的每个产生式重复此步骤。

Step 4 − Replace each production A → B1…Bn where n > 2 with A → B1C where C → B2 …Bn. Repeat this step for all productions having two or more symbols in the right side.

Step 5 − 如果任何产生式的右侧形式为 A → aB ，其中 a 是一个终结符且 A, B 是非终结符，那么该产生式被替换为 A → XB 和 X → a 。对形式为 A → aB 的每个产生式重复此步骤。

Step 5 − If the right side of any production is in the form A → aB where a is a terminal and A, B are non-terminal, then the production is replaced by A → XB and X → a. Repeat this step for every production which is in the form A → aB.

Problem

将以下 CFG 转换为 CNF

Convert the following CFG into CNF

S → ASA | aB, A → B | S, B → b | ε

Solution

(1) 因为 S 出现在 R.H.S 中，我们添加一个新状态 S0 ， S0→S 被添加到产生式集中并变为 −

(1) Since S appears in R.H.S, we add a new state S0 and S0→S is added to the production set and it becomes −

S0→S, S→ ASA | aB, A → B | S, B → b | ∈

(2) 现在我们将删除空发生式 −

(2) Now we will remove the null productions −

B → ∈和 A → ∈

B → ∈ and A → ∈

在删除了 B → ε 后，产生式集变为 −

After removing B → ε, the production set becomes −

S0→S, S→ ASA | aB | a, A → B | S | ∈, B → b

在删除了 A → ∈ 后，产生式集变为 −

After removing A → ∈, the production set becomes −

S0→S, S→ ASA | aB | a | AS | SA | S, A → B | S, B → b

(3) 现在我们将删除单元产生式。

(3) Now we will remove the unit productions.

在删除了 S → S 后，产生式集变为 −

After removing S → S, the production set becomes −

S0→S, S→ ASA | aB | a | AS | SA, A → B | S, B → b

在删除了 S0→ S 后，产生式集变为 −

After removing S0→ S, the production set becomes −

S0→ ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA

A → B | S, B → b

在删除了 A→ B 后，产生式集变为 −

After removing A→ B, the production set becomes −

S0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA

A → S | b

B→b

B → b

移除 A→S 后，产生式集合变为 −

After removing A→ S, the production set becomes −

S0 → ASA | aB | a | AS | SA, S→ ASA | aB | a | AS | SA

A→b |ASA | aB | a | AS | SA，B→b

A → b |ASA | aB | a | AS | SA, B → b

(4) 现在我们将寻找 R.H.S 中有多个变量的项

(4) Now we will find out more than two variables in the R.H.S

此处，S0→ASA、S→ASA、A→ASA 违反了 R.H.S 中的两个非终结符。

Here, S0→ ASA, S → ASA, A→ ASA violates two Non-terminals in R.H.S.

因此，我们将应用步骤 4 和步骤 5 来获得以下在 CNF 中的最终产生式集合 −

Hence we will apply step 4 and step 5 to get the following final production set which is in CNF −

S0→AX | aB | a | AS | SA

S0→ AX | aB | a | AS | SA

S→AX | aB | a | AS | SA

S→ AX | aB | a | AS | SA

A→b |AX | aB | a | AS | SA

A → b |AX | aB | a | AS | SA

B→b

B → b

X→SA

X → SA

(5) 我们必须更改产生式 S0→aB、S→aB、A→aB

(5) We have to change the productions S0→ aB, S→ aB, A→ aB

最终产生式集合变为 −

And the final production set becomes −

S0→AX | YB | a | AS | SA

S0→ AX | YB | a | AS | SA

S→AX | YB | a | AS | SA

S→ AX | YB | a | AS | SA

A→b A→b |AX | YB | a | AS | SA

A → b A → b |AX | YB | a | AS | SA

B→b

B → b

X→SA

X → SA

Y→a

Y → a

Greibach Normal Form

如果产生式具有以下形式，则 CFG 处于 Greibach 范式中 −

A CFG is in Greibach Normal Form if the Productions are in the following forms −

A → b

A → bD1…Dn

S → ε

其中 A、D1、…、Dn 是非终结符，b 是终结符。

where A, D1,….,Dn are non-terminals and b is a terminal.

Algorithm to Convert a CFG into Greibach Normal Form

Step 1 − 如果起始符号 S 出现于某个右侧，创建一个新起始符号 S’ 和一个新产生式 S’ → S 。

Step 1 − If the start symbol S occurs on some right side, create a new start symbol S’ and a new production S’ → S.

Step 2 − 删除空产生式。（使用前面讨论的空产生式消除算法）

Step 2 − Remove Null productions. (Using the Null production removal algorithm discussed earlier)

Step 3 − 删除单位产生式。（使用前面讨论的单位产生式消除算法）

Step 3 − Remove unit productions. (Using the Unit production removal algorithm discussed earlier)

Step 4 − 删除所有直接和间接左递归。

Step 4 − Remove all direct and indirect left-recursion.

Step 5 − 适当替换产生式以将其转换为 GNF 的正确形式。

Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.

Problem

将以下 CFG 转换为 CNF

Convert the following CFG into CNF

S → XY | Xn | p

X → mX | m

Y → Xn | o

Solution

在此， S 未出现在任何产生式的右侧，且产生式规则集中不存在单元或空产生式。因此，我们可以跳过步骤 1 到步骤 3。

Here, S does not appear on the right side of any production and there are no unit or null productions in the production rule set. So, we can skip Step 1 to Step 3.

Step 4

现在，替换以下内容：

Now after replacing

S → XY | Xo | p

X in S → XY | Xo | p

带有

with

mX | m

我们得到：

we obtain

S → mXY | mY | mXo | mo | p。

S → mXY | mY | mXo | mo | p.

然后替换以下内容：

And after replacing

Y → Xn | o

X in Y → Xn | o

为

with the right side of

X → mX | m

我们得到：

we obtain

Y → mXn | mn | o。

Y → mXn | mn | o.

两个新的产生式 O → o 和 P → p 被添加到产生式集中，然后我们得出最终的 GNF，如下所示：

Two new productions O → o and P → p are added to the production set and then we came to the final GNF as the following −

S → mXY | mY | mXC | mC | p

X → mX | m

Y → mXD | mD | o

O → o

P → p

Pumping Lemma for CFG

Lemma

如果 L 是上下文无关语言，那么存在一个泵长 p ，使得任何长度为 ≥ p 的字符串 w ∈ L 均可写为 w = uvxyz ，其中 vy ≠ ε 、 |vxy| ≤ p ，且对于所有 i ≥ 0, uvixyiz ∈ L 。

If L is a context-free language, there is a pumping length p such that any string w ∈ L of length ≥ p can be written as w = uvxyz, where vy ≠ ε, |vxy| ≤ p, and for all i ≥ 0, uvixyiz ∈ L.

Applications of Pumping Lemma

泵引理用于检查语法是否上下文无关。让我们举一个例子来说明它是如何检查的。

Pumping lemma is used to check whether a grammar is context free or not. Let us take an example and show how it is checked.

Problem

找出语言 L = {xnynzn | n ≥ 1} 是否上下文无关。

Find out whether the language L = {xnynzn | n ≥ 1} is context free or not.

Solution

令 L 是无上下文的。然后， L 必须满足抽空引理。

Let L is context free. Then, L must satisfy pumping lemma.

首先，选择抽空引理中的一个数字 n 。然后，将z视为0n1n2n。

At first, choose a number n of the pumping lemma. Then, take z as 0n1n2n.

将 z 分解为 uvwxy, ，其中

Break z into uvwxy, where

|vwx| ≤ n and vx ≠ ε.

因此 vwx 不可能同时包含0和2，因为最后一个0和第一个2至少相隔(n+1)个位置。有两种情况 −

Hence vwx cannot involve both 0s and 2s, since the last 0 and the first 2 are at least (n+1) positions apart. There are two cases −

Case 1 − vwx 没有2。然后 vx 只包含0和1。然后 uwy ，它必须在 L 中，有 n 2，但少于 n 0或1。

Case 1 − vwx has no 2s. Then vx has only 0s and 1s. Then uwy, which would have to be in L, has n 2s, but fewer than n 0s or 1s.

Case 2 − vwx 没有0。

Case 2 − vwx has no 0s.

这里出现了矛盾。

Here contradiction occurs.

因此， L 不是无上下文语言。

Hence, L is not a context-free language.

Pushdown Automata Introduction

Basic Structure of PDA

下推自动机是一种以与我们为正规语法设计DFA类似的方式实现无上下文语法的途径。一个DFA可以记忆有限量的信息，而一个PDA可以记忆无限量的信息。

A pushdown automaton is a way to implement a context-free grammar in a similar way we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.

基本上，下推自动机为 −

Basically a pushdown automaton is −

"Finite state machine" + "a stack"

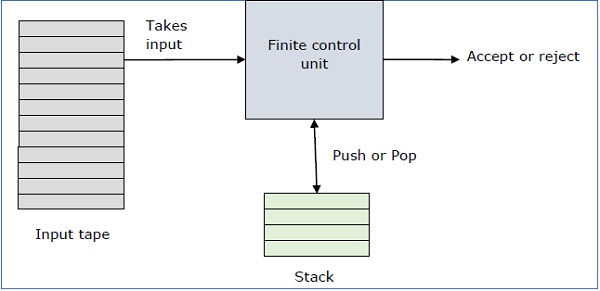
一个下推自动机有三个组件 −

A pushdown automaton has three components −

an input tape,
a control unit, and
a stack with infinite size.

栈头扫描栈的顶端符号。

The stack head scans the top symbol of the stack.

栈执行两种操作 −

A stack does two operations −

Push − a new symbol is added at the top.
Pop − the top symbol is read and removed.

一个PDA可以读取或不读取一个输入符号，但它必须在每个转换中读取栈的顶部。

A PDA may or may not read an input symbol, but it has to read the top of the stack in every transition.

PDA 可以形式化描述为一个 7 元组 (Q, ∑, S, δ, q0, I, F)

A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q0, I, F) −

Q is the finite number of states
∑ is input alphabet
S is stack symbols
δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S*
q0 is the initial state (q0 ∈ Q)
I is the initial stack top symbol (I ∈ S)
F is a set of accepting states (F ∈ Q)

下图展示了一个 PDA 从一个状态 q1 到状态 q2 的转换，标记为 a,b → c

The following diagram shows a transition in a PDA from a state q1 to state q2, labeled as a,b → c −

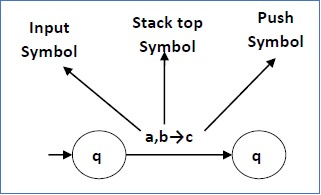
这意味着在状态 q1 ，如果我们遇到一个输入字符串 ‘a’ 且栈顶符号是 ‘b’ ，则我们弹出 ‘b’ ，入栈 ‘c’ 至栈顶，并移至状态 q2 。

This means at state q1, if we encounter an input string ‘a’ and top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q2.

Terminologies Related to PDA

Instantaneous Description

PDA 的瞬时描述（ID）由三元组 (q, w, s) 表示，其中

The instantaneous description (ID) of a PDA is represented by a triplet (q, w, s) where

q is the state
w is unconsumed input
s is the stack contents

Turnstile Notation

“turnstile”符号用于连接表示 PDA 的一次或多次移动的 ID 对。转换过程由 turnstile 符号“⊢”表示。

The "turnstile" notation is used for connecting pairs of ID’s that represent one or many moves of a PDA. The process of transition is denoted by the turnstile symbol "⊢".

考虑一个 PDA (Q, ∑, S, δ, q0, I, F)。一个转换可以用下面的 turnstile 符号以数学方式表示

Consider a PDA (Q, ∑, S, δ, q0, I, F). A transition can be mathematically represented by the following turnstile notation −

(p, aw, Tβ) ⊢ (q, w, αb)

这表示在从状态 p 转换到状态 q 时，消耗了输入符号 ‘a’ ，且栈顶 ‘T’ 被一个新字符串 ‘α’ 替换。

This implies that while taking a transition from state p to state q, the input symbol ‘a’ is consumed, and the top of the stack ‘T’ is replaced by a new string ‘α’.

Note - 如果希望 PDA 的移动次数为零或更多，则必须使用符号 (⊢*)。

Note − If we want zero or more moves of a PDA, we have to use the symbol (⊢*) for it.

Pushdown Automata Acceptance

可以用两种不同的方式定义 PDA 可接受性。

There are two different ways to define PDA acceptability.

Final State Acceptability

在最终状态可接受性中，当读取完整个字符串后，如果 PDA 处于最终状态，则 PDA 接受一个字符串。从开始状态，我们可以采取最终停留在最终状态的步骤，而无论栈值是什么。只要我们最终处于最终状态，那么栈值就无关紧要。

In final state acceptability, a PDA accepts a string when, after reading the entire string, the PDA is in a final state. From the starting state, we can make moves that end up in a final state with any stack values. The stack values are irrelevant as long as we end up in a final state.

对于 PDA (Q, ∑, S, δ, q0, I, F)，结束状态 F 集合接受的语言为 −

For a PDA (Q, ∑, S, δ, q0, I, F), the language accepted by the set of final states F is −

L(PDA) = {w | (q0, w, I) ⊢* (q, ε, x), q ∈ F}

对于任何输入的栈字符串 x 。

for any input stack string x.

Empty Stack Acceptability

此处 PDA 在读取完整个字符串后，如果 PDA 清空了栈，则接受一个字符串。

Here a PDA accepts a string when, after reading the entire string, the PDA has emptied its stack.

对于 PDA (Q, ∑, S, δ, q0, I, F)，空栈接受的语言为 −

For a PDA (Q, ∑, S, δ, q0, I, F), the language accepted by the empty stack is −

L(PDA) = {w | (q0, w, I) ⊢* (q, ε, ε), q ∈ Q}

Example

构造一个接受 L = {0n 1n | n ≥ 0} 的 PDA

Construct a PDA that accepts L = {0n 1n | n ≥ 0}

Solution

本语言接受 L = {ε, 01, 0011, 000111, ……………………….. }

This language accepts L = {ε, 01, 0011, 000111, ……………………….. }

在此示例中， ‘a’ 和 ‘b’ 的数量必须相同。

Here, in this example, the number of ‘a’ and ‘b’ have to be same.

Initially we put a special symbol ‘$’ into the empty stack.
Then at state q2, if we encounter input 0 and top is Null, we push 0 into stack. This may iterate. And if we encounter input 1 and top is 0, we pop this 0.
Then at state q3, if we encounter input 1 and top is 0, we pop this 0. This may also iterate. And if we encounter input 1 and top is 0, we pop the top element.
If the special symbol ‘$’ is encountered at top of the stack, it is popped out and it finally goes to the accepting state q4.

Example

构造一个 PDA 接受 L = { wwR | w = (a+b)* }

Construct a PDA that accepts L = { wwR | w = (a+b)* }

Solution

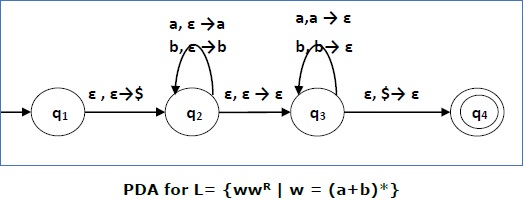
最初我们在空栈中添加一个特殊符号“$”。在状态 q2 中，正在读取 w 。在状态 w 中，每个 0 或 1 在与输入匹配时弹出。如果给出了任何其他输入，则 PDA 将进入死状态。当我们到达该特殊符号“$”时，我们进入接受状态 q3 。

Initially we put a special symbol ‘$’ into the empty stack. At state q2, the w is being read. In state q3, each 0 or 1 is popped when it matches the input. If any other input is given, the PDA will go to a dead state. When we reach that special symbol ‘$’, we go to the accepting state q4.

PDA & Context-Free Grammar

如果一个语法 G 是无上下文的，我们可以构建一个等效的非确定性 PDA，它接受由无上下文语法 G 生成的语言。可以为语法 G 构建一个解析器。

If a grammar G is context-free, we can build an equivalent nondeterministic PDA which accepts the language that is produced by the context-free grammar G. A parser can be built for the grammar G.

另外，如果 P 是下推机，则可以构建一个等效的无上下文语法 G，其中

Also, if P is a pushdown automaton, an equivalent context-free grammar G can be constructed where

L(G) = L(P)

在接下来的两个主题中，我们将讨论如何从 PDA 转换为 CFG，反之亦然。

In the next two topics, we will discuss how to convert from PDA to CFG and vice versa.

Algorithm to find PDA corresponding to a given CFG

Input - 一个 CFG，G = (V, T, P, S)

Input − A CFG, G = (V, T, P, S)

Output − 等价的 PDA，P = (Q, ∑, S, δ, q0, I, F)

Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F)

Step 1 − 将 CFG 的产生式转换成 GNF。

Step 1 − Convert the productions of the CFG into GNF.

Step 2 − PDA 将只有唯一状态 {q}。

Step 2 − The PDA will have only one state {q}.

Step 3 − CFG 的起始符号将是 PDA 中的起始符号。

Step 3 − The start symbol of CFG will be the start symbol in the PDA.

Step 4 − CFG的所有非终结符号将是 PDA 的栈符号，且 CFG 的所有终结符号将是 PDA 的输入符号。

Step 4 − All non-terminals of the CFG will be the stack symbols of the PDA and all the terminals of the CFG will be the input symbols of the PDA.

Step 5 − 对于形式 A → aX 的每个产生式，其中 a 为终结符， A, X 是终结符和非终结符的组合，创建转换 δ (q, a, A) 。

Step 5 − For each production in the form A → aX where a is terminal and A, X are combination of terminal and non-terminals, make a transition δ (q, a, A).

Problem

根据以下 CFG 构建一个 PDA。

Construct a PDA from the following CFG.

G = ({S, X}, {a, b}, P, S)

其产生式为−

where the productions are −

S → XS | ε , A → aXb | Ab | ab

Solution

让等价 PDA 为，

Let the equivalent PDA,

P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)

其中 δ −

where δ −

δ(q, ε , S) = {(q, XS), (q, ε )}

δ(q, ε , X) = {(q, aXb), (q, Xb), (q, ab)}

δ(q, a, a) = {(q, ε )}

δ(q, 1, 1) = {(q, ε )}

Algorithm to find CFG corresponding to a given PDA

Input - 一个 CFG，G = (V, T, P, S)

Input − A CFG, G = (V, T, P, S)

Output − 等价的 PDA，P = (Q, ∑, S, δ, q0, I, F)，其中语法 G 的非终结符为 {Xwx | w,x ∈ Q}，开始状态为 Aq0,F。

Output − Equivalent PDA, P = (Q, ∑, S, δ, q0, I, F) such that the non- terminals of the grammar G will be {Xwx | w,x ∈ Q} and the start state will be Aq0,F.

Step 1 − 对于 Q 中的每个 w、x、y、z，S 中的 m 以及 ∑ 中的 a、b，如果 δ (w, a, ε) 包含 (y, m) 且 (z, b, m) 包含 (x, ε) ，则在语法 G 中添加产生式规则 Xwx → a Xyzb。

Step 1 − For every w, x, y, z ∈ Q, m ∈ S and a, b ∈ ∑, if δ (w, a, ε) contains (y, m) and (z, b, m) contains (x, ε), add the production rule Xwx → a Xyzb in grammar G.

Step 2 - 对于任意 Q 中的 w、x、y、z，在语法 G 中添加产生式 Xwx → XwyXyx。

Step 2 − For every w, x, y, z ∈ Q, add the production rule Xwx → XwyXyx in grammar G.

Step 3 - 对于 Q 中的 w，在语法 G 中添加产生式 Xww → ε。

Step 3 − For w ∈ Q, add the production rule Xww → ε in grammar G.

Pushdown Automata & Parsing

解析用于根据语法的产生式导出一串字符。它用于检查一串字符的可接受性。编译器用于检查一串字符在语法上是否正确。解析器获取输入并构建一个解析树。

Parsing is used to derive a string using the production rules of a grammar. It is used to check the acceptability of a string. Compiler is used to check whether or not a string is syntactically correct. A parser takes the inputs and builds a parse tree.

解析器可以分为两种类型 -

A parser can be of two types −

Top-Down Parser − Top-down parsing starts from the top with the start-symbol and derives a string using a parse tree.
Bottom-Up Parser − Bottom-up parsing starts from the bottom with the string and comes to the start symbol using a parse tree.

Design of Top-Down Parser

对于自顶向下解析，PDA 有以下四种类型的转换 -

For top-down parsing, a PDA has the following four types of transitions −

Pop the non-terminal on the left hand side of the production at the top of the stack and push its right-hand side string.
If the top symbol of the stack matches with the input symbol being read, pop it.
Push the start symbol ‘S’ into the stack.
If the input string is fully read and the stack is empty, go to the final state ‘F’.

Example

设计一个自顶向下的解析器来解析表达式“x+y*z”，针对具有以下产生式的语法 G -

Design a top-down parser for the expression "x+y*z" for the grammar G with the following production rules −

P: S → S+X | X, X → X*Y | Y, Y → (S) | id

Solution

如果 PDA 为 (Q, ∑, S, δ, q0, I, F)，则自顶向下的解析如下 -

If the PDA is (Q, ∑, S, δ, q0, I, F), then the top-down parsing is −

(x+y*z, I) ⊢(x +y*z, SI) ⊢ (x+y*z, S+XI) ⊢(x+y*z, X+XI)

⊢(x+y*z, Y+X I) ⊢(x+y*z, x+XI) ⊢(+y*z, +XI) ⊢ (y*z, XI)

⊢(y*z, X*YI) ⊢(y*z, y*YI) ⊢(*z,*YI) ⊢(z, YI) ⊢(z, zI) ⊢(ε, I)

Design of a Bottom-Up Parser

对于自底向上解析，PDA 具有以下四种类型的转换 -

For bottom-up parsing, a PDA has the following four types of transitions −

Push the current input symbol into the stack.
Replace the right-hand side of a production at the top of the stack with its left-hand side.
If the top of the stack element matches with the current input symbol, pop it.
If the input string is fully read and only if the start symbol ‘S’ remains in the stack, pop it and go to the final state ‘F’.

Example

设计一个自顶向下的解析器来解析表达式“x+y*z”，针对具有以下产生式的语法 G -

Design a top-down parser for the expression "x+y*z" for the grammar G with the following production rules −

P：S → S+X | X，X → X*Y | Y，Y →（S）| id

P: S → S+X | X, X → X*Y | Y, Y → (S) | id

Solution

如果 PDA 是 (Q，∑，S，δ，q0，I，F)，则自底向上解析如下所示 −

If the PDA is (Q, ∑, S, δ, q0, I, F), then the bottom-up parsing is −

(x+y*z, I) ⊢ (+y*z, xI) ⊢ (+y*z, YI) ⊢ (+y*z, XI) ⊢ (+y*z, SI)

⊢(y*z, +SI) ⊢ (*z, y+SI) ⊢ (*z, Y+SI) ⊢ (*z, X+SI) ⊢ (z, *X+SI)

⊢ (ε, z*X+SI) ⊢ (ε, Y*X+SI) ⊢ (ε, X+SI) ⊢ (ε, SI)

Turing Machine Introduction

图灵机是一种接受设备，它接受由类型 0 语法生成的语言（递归可枚举集合）。它是由艾伦·图灵于 1936 年发明的。

A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type 0 grammars. It was invented in 1936 by Alan Turing.

Definition

图灵机 ™ 是一种数学模型，它由一条分成小格子的无限长胶带组成，输入内容写在胶带上。它包含一个用来读取输入胶带磁头的。状态寄存器存储图灵机的状态。在读取输入符号之后，它会用其他符号替换该符号，改变其内部状态，并向右或向左移动一个单元格。如果 TM 达到最终状态，则接受输入字符串，否则拒绝。

A Turing Machine ™ is a mathematical model which consists of an infinite length tape divided into cells on which input is given. It consists of a head which reads the input tape. A state register stores the state of the Turing machine. After reading an input symbol, it is replaced with another symbol, its internal state is changed, and it moves from one cell to the right or left. If the TM reaches the final state, the input string is accepted, otherwise rejected.

TM 可以形式上描述为一个 7 元组 (Q，X，∑，δ，q0，B，F)，其中 −

A TM can be formally described as a 7-tuple (Q, X, ∑, δ, q0, B, F) where −

Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function; δ : Q × X → Q × X × {Left_shift, Right_shift}.
q0 is the initial state
B is the blank symbol
F is the set of final states

Comparison with the previous automaton

下表展示了图灵机与有限状态机和下推自动机的不同之处。

The following table shows a comparison of how a Turing machine differs from Finite Automaton and Pushdown Automaton.

Machine

Stack Data Structure

Deterministic?

Finite Automaton

N.A

Yes

Pushdown Automaton

Last In First Out(LIFO)

Turing Machine

Infinite tape

Yes

Example of Turing machine

图灵机 M = (Q，X，∑，δ，q0，B，F) 带有

Turing machine M = (Q, X, ∑, δ, q0, B, F) with

Q = {q0, q1, q2, qf}
X = {a, b}
∑ = {1}
q0 = {q0}
B = blank symbol
F = {qf }

δ 由 − 给出

δ is given by −

Tape alphabet symbol

Present State ‘q0’

Present State ‘q1’

Present State ‘q2’

1Rq1

1Lq0

1Lqf

1Lq2

1Rq1

1Rqf

这里的转移 1Rq1 表示写入符号是 1，胶带向右移动，下一个状态是 q1。同样，转移 1Lq2 表示写入符号是 1，胶带向左移动，下一个状态是 q2。

Here the transition 1Rq1 implies that the write symbol is 1, the tape moves right, and the next state is q1. Similarly, the transition 1Lq2 implies that the write symbol is 1, the tape moves left, and the next state is q2.

Time and Space Complexity of a Turing Machine

对于图灵机，时间复杂度指代机器针对某些输入符号初始化时，磁带移动次数的度量，空间复杂度是指磁带上书写单元格的数量。

For a Turing machine, the time complexity refers to the measure of the number of times the tape moves when the machine is initialized for some input symbols and the space complexity is the number of cells of the tape written.

时间复杂度所有合理函数 −

Time complexity all reasonable functions −

T(n) = O(n log n)

TM 的空间复杂性 −

TM’s space complexity −

S(n) = O(n)

Accepted Language & Decided Language

如果对任何输入字符串 w 都进入最终状态，那么 TM 会接受一种语言。如果图灵机接受一种语言，则该语言是递归可枚举的（由 0 型语法生成）。

A TM accepts a language if it enters into a final state for any input string w. A language is recursively enumerable (generated by Type-0 grammar) if it is accepted by a Turing machine.

如果 TM 接受一种语言并且对语言中不存在的任何输入进入一个拒绝状态，则该 TM 判定一种语言。如果图灵机判定一种语言，则该语言是递归的。

A TM decides a language if it accepts it and enters into a rejecting state for any input not in the language. A language is recursive if it is decided by a Turing machine.

在某些情况下，TM 可能不会停止。此类 TM 会接受该语言，但不会判定它。

There may be some cases where a TM does not stop. Such TM accepts the language, but it does not decide it.

Designing a Turing Machine

下面已借助几个示例说明了设计图灵机的基本准则。

The basic guidelines of designing a Turing machine have been explained below with the help of a couple of examples.

Example 1

设计能够识别由奇数个 α 组成的所有字符串的 TM。

Design a TM to recognize all strings consisting of an odd number of α’s.

Solution

图灵机 M 可以通过以下动作构建 −

The Turing machine M can be constructed by the following moves −

Let q1 be the initial state.
If M is in q1; on scanning α, it enters the state q2 and writes B (blank).
If M is in q2; on scanning α, it enters the state q1 and writes B (blank).
From the above moves, we can see that M enters the state q1 if it scans an even number of α’s, and it enters the state q2 if it scans an odd number of α’s. Hence q2 is the only accepting state.

因此，

Hence,

M = {{q1, q2}, {1}, {1, B}, δ, q1, B, {q2}}

其中 δ 表示为 −

where δ is given by −

Tape alphabet symbol

Present State ‘q1’

Present State ‘q2’

BRq2

BRq1

Example 2

设计读取表示二进制数的字符串并消除字符串中所有前置 0 的图灵机。但是，如果字符串仅包含 0，则它会保留一个 0。

Design a Turing Machine that reads a string representing a binary number and erases all leading 0’s in the string. However, if the string comprises of only 0’s, it keeps one 0.

Solution

我们假设输入字符串在字符串的每端都由空格符号 B 终止。

Let us assume that the input string is terminated by a blank symbol, B, at each end of the string.

图灵机 M 可以通过以下动作构建 −

The Turing Machine, M, can be constructed by the following moves −

Let q0 be the initial state.
If M is in q0, on reading 0, it moves right, enters the state q1 and erases 0. On reading 1, it enters the state q2 and moves right.
If M is in q1, on reading 0, it moves right and erases 0, i.e., it replaces 0’s by B’s. On reaching the leftmost 1, it enters q2 and moves right. If it reaches B, i.e., the string comprises of only 0’s, it moves left and enters the state q3.
If M is in q2, on reading either 0 or 1, it moves right. On reaching B, it moves left and enters the state q4. This validates that the string comprises only of 0’s and 1’s.
If M is in q3, it replaces B by 0, moves left and reaches the final state qf.
If M is in q4, on reading either 0 or 1, it moves left. On reaching the beginning of the string, i.e., when it reads B, it reaches the final state qf.

因此，

Hence,

M = {{q0, q1, q2, q3, q4, qf}, {0,1, B}, {1, B}, δ, q0, B, {qf}}

其中 δ 表示为 −

where δ is given by −

Tape alphabet symbol

Present State ‘q0’

Present State ‘q1’

Present State ‘q2’

Present State ‘q3’

Present State ‘q4’

BRq1

ORq2

OLq4

1Rq2

1Lq4

BRq1

BLq3

BLq4

OLqf

BRqf

Multi-tape Turing Machine

多磁带图灵机有多个磁带，每个磁带都通过一个单独的磁头进行访问。每个磁头可以独立于其他磁头移动。最初输入在磁带 1 上，其他磁带为空。一开始，第一磁带被输入占据，其他磁带保持空白。接下来，机器读取其磁头下的连续符号，TM 在每个磁带上打印一个符号并移动其磁头。

Multi-tape Turing Machines have multiple tapes where each tape is accessed with a separate head. Each head can move independently of the other heads. Initially the input is on tape 1 and others are blank. At first, the first tape is occupied by the input and the other tapes are kept blank. Next, the machine reads consecutive symbols under its heads and the TM prints a symbol on each tape and moves its heads.

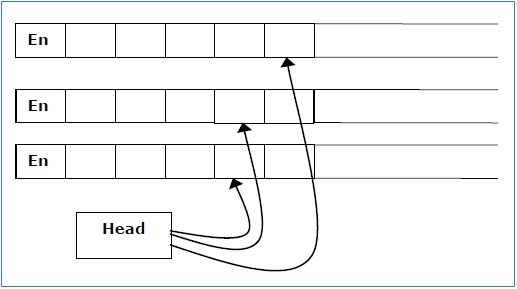
多磁带图灵机可正式描述为 6 元组 (Q, X, B, δ, q0, F)，其中 -

A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −

Q is a finite set of states
X is the tape alphabet
B is the blank symbol
δ is a relation on states and symbols where δ: Q × Xk → Q × (X × {Left_shift, Right_shift, No_shift })k where there is k number of tapes
q0 is the initial state
F is the set of final states

Note - 每个多磁带图灵机都有一个等效的单磁带图灵机。

Note − Every Multi-tape Turing machine has an equivalent single-tape Turing machine.

Multi-track Turing Machine

多轨图灵机是多磁带图灵机的特定类型，它包含多个磁道，但只有一个磁头可以读取和写入所有磁道。在此，单个磁头可以一步从 n 个磁道中读取 n 个符号。它接受递归可枚举语言，就像普通单轨单带图灵机所接受的一样。

Multi-track Turing machines, a specific type of Multi-tape Turing machine, contain multiple tracks but just one tape head reads and writes on all tracks. Here, a single tape head reads n symbols from n tracks at one step. It accepts recursively enumerable languages like a normal single-track single-tape Turing Machine accepts.

多轨图灵机可以正式描述为一个 6 元组 (Q, X, ∑, δ, q0, F)，其中 −

A Multi-track Turing machine can be formally described as a 6-tuple (Q, X, ∑, δ, q0, F) where −

Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a relation on states and symbols where δ(Qi, [a1, a2, a3,….]) = (Qj, [b1, b2, b3,….], Left_shift or Right_shift)
q0 is the initial state
F is the set of final states

Note − 对于每一个单轨图灵机 S ，都有一个等价的多轨图灵机 M ，使得 L(S) = L(M) 。

Note − For every single-track Turing Machine S, there is an equivalent multi-track Turing Machine M such that L(S) = L(M).

Non-Deterministic Turing Machine

在非确定图灵机中，对于每个状态和符号，TM 有一组操作。因此，这里的转换不是确定的。非确定图灵机的计算是从开始配置可以到达的一系列配置树。

In a Non-Deterministic Turing Machine, for every state and symbol, there are a group of actions the TM can have. So, here the transitions are not deterministic. The computation of a non-deterministic Turing Machine is a tree of configurations that can be reached from the start configuration.

如果树至少有一个节点是接受配置，则接受输入，否则不接受。如果计算树的所有分支在所有输入上停止，则非确定图灵机被称为 Decider ，如果对于某个输入，所有分支都被拒绝，则输入也被拒绝。

An input is accepted if there is at least one node of the tree which is an accept configuration, otherwise it is not accepted. If all branches of the computational tree halt on all inputs, the non-deterministic Turing Machine is called a Decider and if for some input, all branches are rejected, the input is also rejected.

一个非确定图灵机可以形式地定义为一个 6 元组 (Q, X, ∑, δ, q0, B, F)，其中 -

A non-deterministic Turing machine can be formally defined as a 6-tuple (Q, X, ∑, δ, q0, B, F) where −

Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function; δ : Q × X → P(Q × X × {Left_shift, Right_shift}).
q0 is the initial state
B is the blank symbol
F is the set of final states

Semi-Infinite Tape Turing Machine

具有半无限磁带的图灵机具有左端但没有右端。左端用结束标记限制。

A Turing Machine with a semi-infinite tape has a left end but no right end. The left end is limited with an end marker.

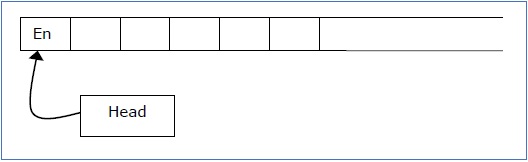
它是一条两轨磁带 -

It is a two-track tape −

Upper track − It represents the cells to the right of the initial head position.
Lower track − It represents the cells to the left of the initial head position in reverse order.

无限长度的输入字符串最初写在磁带的连续磁带单元格中。

The infinite length input string is initially written on the tape in contiguous tape cells.

机器从初始状态 q0 开始，磁头从左端标记“结束”开始扫描。在每个步骤中，它读取磁头下方磁带上的符号。它在该磁带单元格上写一个新符号，然后将磁头向左或向右移动一个磁带单元格。转换函数决定要采取的操作。

The machine starts from the initial state q0 and the head scans from the left end marker ‘End’. In each step, it reads the symbol on the tape under its head. It writes a new symbol on that tape cell and then it moves the head either into left or right one tape cell. A transition function determines the actions to be taken.

它有两个称为 accept state 和 reject state 的特殊状态。如果在任何时间点进入接受状态，则接受输入；如果进入拒绝状态，则 TM 拒绝输入。在某些情况下，它会继续无限运行，而不会被某些特定输入符号接受或拒绝。

It has two special states called accept state and reject state. If at any point of time it enters into the accepted state, the input is accepted and if it enters into the reject state, the input is rejected by the TM. In some cases, it continues to run infinitely without being accepted or rejected for some certain input symbols.

Note - 带有半无限磁带的图灵机与标准图灵机等效。

Note − Turing machines with semi-infinite tape are equivalent to standard Turing machines.

Linear Bounded Automata

线性有界自动机是一个多轨非确定性图灵机，其磁带具有某种有界有限长度。

A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some bounded finite length.

Length = function (Length of the initial input string, constant c)

在此，

Here,

Memory information ≤ c × Input information

计算受限于常量有界区域。输入字母表包含两个特殊符号，用作左端标记和右端标记，这意味着转换既不会移动到左端标记的左边，也不会移动到磁带右端标记的右边。

The computation is restricted to the constant bounded area. The input alphabet contains two special symbols which serve as left end markers and right end markers which mean the transitions neither move to the left of the left end marker nor to the right of the right end marker of the tape.

线性有界自动机可以定义为 8 元组 (Q, X, ∑, q0, ML, MR, δ, F)，其中 −

A linear bounded automaton can be defined as an 8-tuple (Q, X, ∑, q0, ML, MR, δ, F) where −

Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
q0 is the initial state
ML is the left end marker
MR is the right end marker where MR ≠ ML
δ is a transition function which maps each pair (state, tape symbol) to (state, tape symbol, Constant ‘c’) where c can be 0 or +1 or -1
F is the set of final states

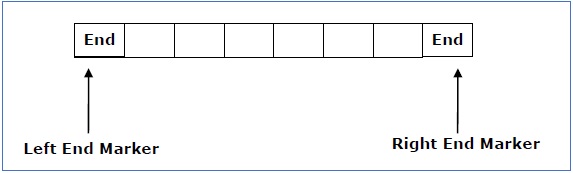
确定性线性有界自动机总是 context-sensitive ，而空语言线性有界自动机是 undecidable. 。

A deterministic linear bounded automaton is always context-sensitive and the linear bounded automaton with empty language is undecidable..

Language Decidability

如果存在一台图灵机，接受并停止处理每个输入字符串 w ，则称为 Decidable 或 Recursive 语言。每个可判定的语言都是图灵可接受的。

A language is called Decidable or Recursive if there is a Turing machine which accepts and halts on every input string w. Every decidable language is Turing-Acceptable.

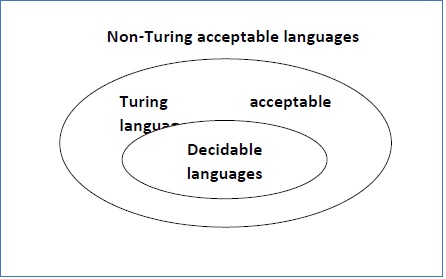
如果所有“是”例子的语言 L 是可判定的，则判定问题 P 是可判定的。

A decision problem P is decidable if the language L of all yes instances to P is decidable.

对于可判定的语言，针对每个输入字符串，TM 在接受或拒绝状态停止处理，如下图所示 −

For a decidable language, for each input string, the TM halts either at the accept or the reject state as depicted in the following diagram −

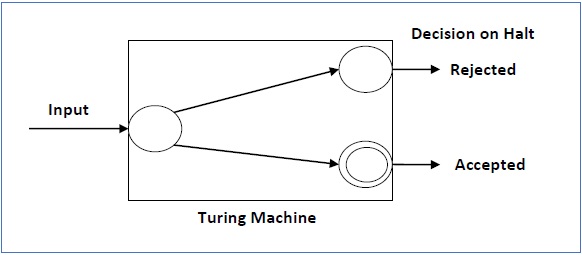
Example 1

找出以下问题是否可判定的 −

Find out whether the following problem is decidable or not −

数字“m”是否为素数？

Is a number ‘m’ prime?

Solution

素数 = {2, 3, 5, 7, 11, 13, …………..}

Prime numbers = {2, 3, 5, 7, 11, 13, …………..}

将数字 ‘m’ 除以从“2”到“√m”之间的所有数字，从“2”开始。

Divide the number ‘m’ by all the numbers between ‘2’ and ‘√m’ starting from ‘2’.

如果任何这些数字产生余数为零，则转到“拒绝状态”，否则转到“接受状态”。因此，答案可以是“是”或“否”。

If any of these numbers produce a remainder zero, then it goes to the “Rejected state”, otherwise it goes to the “Accepted state”. So, here the answer could be made by ‘Yes’ or ‘No’.

Hence, it is a decidable problem.

Example 2

给定正则语言 L 和字符串 w ，我们如何检查是否 w ∈ L ？

Given a regular language L and string w, how can we check if w ∈ L?

Solution

取接受 L 的 DFA，并检查是否接受 w

Take the DFA that accepts L and check if w is accepted

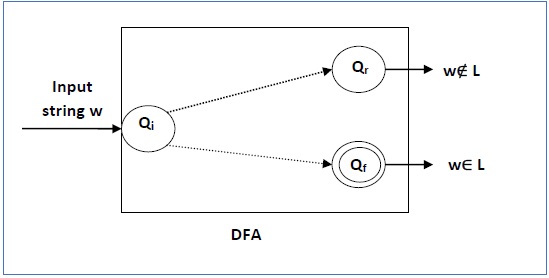
另一些可判定的问题为 −

Some more decidable problems are −

Does DFA accept the empty language?
Is L1 ∩ L2 = ∅ for regular sets?

Note −

If a language L is decidable, then its complement L' is also decidable
If a language is decidable, then there is an enumerator for it.

Undecidable Languages

对于不可判定的语言，不存在接受该语言和对每个输入串 w 做出判定的图灵机（尽管 TM 可以对某些输入串做出判定）。如果对 P 的所有肯定实例的语言 L 是不可判定的，则判定问题 P 称为“不可判定”。不可判定语言不是递归语言，但有时可能是递归可枚举语言。

For an undecidable language, there is no Turing Machine which accepts the language and makes a decision for every input string w (TM can make decision for some input string though). A decision problem P is called “undecidable” if the language L of all yes instances to P is not decidable. Undecidable languages are not recursive languages, but sometimes, they may be recursively enumerable languages.

Example

The halting problem of Turing machine
The mortality problem
The mortal matrix problem
The Post correspondence problem, etc.

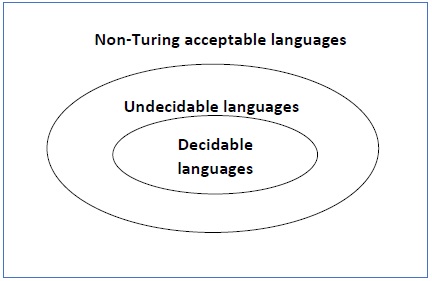
Turing Machine Halting Problem

Input - 图灵机和输入串 w 。

Input − A Turing machine and an input string w.

Problem - 图灵机是否在有限步数中完成字符串 w 的计算？答案必须是肯定或否定。

Problem − Does the Turing machine finish computing of the string w in a finite number of steps? The answer must be either yes or no.

Proof - 首先，我们将假设存在这样的图灵机来解决此问题，然后我们将证明这是自相矛盾的。我们将称此图灵机为 Halting machine ，它在有限时间内生成“是”或“否”。如果求解器在有限时间内完成，则输出结果为“是”，否则为“否”。以下是求解器的框图 −

Proof − At first, we will assume that such a Turing machine exists to solve this problem and then we will show it is contradicting itself. We will call this Turing machine as a Halting machine that produces a ‘yes’ or ‘no’ in a finite amount of time. If the halting machine finishes in a finite amount of time, the output comes as ‘yes’, otherwise as ‘no’. The following is the block diagram of a Halting machine −

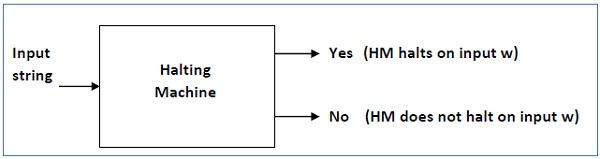
现在，我们将设计一个 inverted halting machine (HM)’ 为 −

Now we will design an inverted halting machine (HM)’ as −

If H returns YES, then loop forever.
If H returns NO, then halt.

以下是“逆求解器”的框图 −

The following is the block diagram of an ‘Inverted halting machine’ −

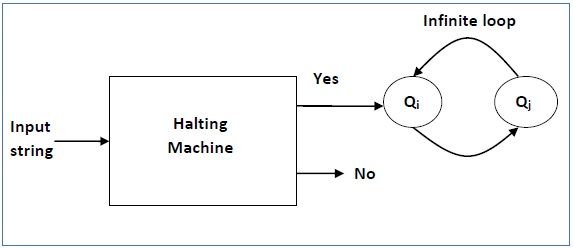
此外，构建了一台将自身作为输入的机器 (HM)2 ，如下所示 −

Further, a machine (HM)2 which input itself is constructed as follows −

If (HM)2 halts on input, loop forever.
Else, halt.

在此，我们得到了一个矛盾。因此，求解问题是 undecidable 。

Here, we have got a contradiction. Hence, the halting problem is undecidable.

Rice Theorem

Rice 定理指出，由图灵机识别的语言任何非平凡语义属性都是不可判定的。一个属性 P 是满足该属性的所有图灵机的语言。

Rice theorem states that any non-trivial semantic property of a language which is recognized by a Turing machine is undecidable. A property, P, is the language of all Turing machines that satisfy that property.

Formal Definition

如果 P 是一个非平凡属性而语言持有属性，Lp，由图灵机 M 识别，则 Lp = {<M> | L(M) ∈ P} 是不可判定的。

If P is a non-trivial property, and the language holding the property, Lp , is recognized by Turing machine M, then Lp = {<M> | L(M) ∈ P} is undecidable.

Description and Properties

Property of languages, P, is simply a set of languages. If any language belongs to P (L ∈ P), it is said that L satisfies the property P.
A property is called to be trivial if either it is not satisfied by any recursively enumerable languages, or if it is satisfied by all recursively enumerable languages.
A non-trivial property is satisfied by some recursively enumerable languages and are not satisfied by others. Formally speaking, in a non-trivial property, where L ∈ P, both the following properties hold: Property 1 − There exists Turing Machines, M1 and M2 that recognize the same language, i.e. either ( <M1>, <M2> ∈ L ) or ( <M1>,<M2> ∉ L ) Property 2 − There exists Turing Machines M1 and M2, where M1 recognizes the language while M2 does not, i.e. <M1> ∈ L and <M2> ∉ L

Proof

假设一个属性P为非平凡的且 φ ∈ P。

Suppose, a property P is non-trivial and φ ∈ P.

由于P为非平凡的，所以至少有一门语言满足P，即L(M0) ∈ P，此图灵机为M0。

Since, P is non-trivial, at least one language satisfies P, i.e., L(M0) ∈ P , ∋ Turing Machine M0.

不妨设w是一个特定时刻的输入，N是一台图灵机，它遵循−

Let, w be an input in a particular instant and N is a Turing Machine which follows −

由输入x

On input x

Run M on w
If M does not accept (or doesn’t halt), then do not accept x (or do not halt)
If M accepts w then run M0 on x. If M0 accepts x, then accept x.

一个函数将一个实例ATM = {<M,w>| M接受输入w}映射到一个N，使得

A function that maps an instance ATM = {<M,w>| M accepts input w} to a N such that

If M accepts w and N accepts the same language as M0, Then L(M) = L(M0) ∈ p
If M does not accept w and N accepts φ, Then L(N) = φ ∉ p

由于ATM是不可判定性的，并且它可以简化为Lp，因此Lp也是不可判定性的。

Since ATM is undecidable and it can be reduced to Lp, Lp is also undecidable.

Post Correspondence Problem

在1946年，Emil Post提出了邮递对应问题（PCP），这是一个不可判定性的判定问题。对于一个字母表∑，PCP问题的描述如下−

The Post Correspondence Problem (PCP), introduced by Emil Post in 1946, is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −

给定以下两个列表，在∑上的非空字符串的 M 和 N −

Given the following two lists, M and N of non-empty strings over ∑ −

M = (x1, x2, x3,………, xn)

N = (y1, y2, y3,………, yn)

我们可以说存在一个后缀对应解决方案，如果对于一些 i1,i2,………… ik，其中 1 ≤ ij ≤ n，条件 xi1 …….xik = yi1 …….yik 得到满足。

We can say that there is a Post Correspondence Solution, if for some i1,i2,………… ik, where 1 ≤ ij ≤ n, the condition xi1 …….xik = yi1 …….yik satisfies.

Example 1

找出列表

Find whether the lists

M = (abb, aa, aaa) 和 N = (bba, aaa, aa)

M = (abb, aa, aaa) and N = (bba, aaa, aa)

是否有后缀对应解？

have a Post Correspondence Solution?

Solution

Abb

aaa

Bba

aaa

在此，

Here,

x2x1x3 = ‘aaabbaaa’

及 y2y1y3 = ‘aaabbaaa’

and y2y1y3 = ‘aaabbaaa’

可以看出

We can see that

x2x1x3 = y2y1y3

因此，解为 i = 2, j = 1, and k = 3.

Hence, the solution is i = 2, j = 1, and k = 3.

Example 2

找出列表 M = (ab, bab, bbaaa) 和 N = (a, ba, bab) 是否有后缀对应解？

Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post Correspondence Solution?

Solution

bab

bbaaa

bab

在这种情况下，没有解，因为 −

In this case, there is no solution because −

| x2x1x3 | ≠ | y2y1y3 | （长度不相同）

| x2x1x3 | ≠ | y2y1y3 | (Lengths are not same)

因此可以说，这个后缀对应问题是 undecidable 。

Hence, it can be said that this Post Correspondence Problem is undecidable.