Digital-electronics 简明教程
BCD to Decimal Converter
一个能将二进制编码十进制 (BCD) 数转换成等效十进制数的数字电路称为 BCD-to-decimal converter 。
BCD 到十进制转换器的输入是一个 8421 BCD 代码，转换器产生的输出是一个十进制数。
以下是 BCD 到十进制转换器的真值表，描述了其工作原理。
BCD Code |
Decimal |
B3 |
B2 |
B1 |
B0 |
0 |
0 |
0 |
0 |
D0 |
0 |
0 |
0 |
1 |
D1 |
0 |
0 |
1 |
0 |
D2 |
0 |
0 |
1 |
1 |
D3 |
0 |
1 |
0 |
0 |
D4 |
0 |
1 |
0 |
1 |
D5 |
0 |
1 |
1 |
0 |
D6 |
0 |
1 |
1 |
1 |
D7 |
1 |
0 |
0 |
0 |
D8 |
1 |
0 |
0 |
1 |
D9 |
我们可以用 8421 BCD 代码来推导出每个十进制输出的布尔表达式。这些布尔表达式如下所示——
\mathrm{D_{0} \: = \: \overline{B_{3}} \: \overline{B_{2}} \: \overline{B_{1}} \: \overline{B_{0}}}
\mathrm{D_{1} \: = \: \overline{B_{3}} \: \overline{B_{2}} \: \overline{B_{1}} \: B_{0}}
\mathrm{D_{2} \: = \: \overline{B_{3}} \: \overline{B_{2}} \: B_{1} \: \overline{B_{0}}}
\mathrm{D_{3} \: = \: \overline{B_{3}} \: \overline{B_{2}} \: B_{1} \: B_{0}}
\mathrm{D_{4} \: = \: \overline{B_{3}} \: B_{2} \: \overline{B_{1}} \: \overline{B_{0}}}
\mathrm{D_{5} \: = \: \overline{B_{3}} \: B_{2} \: \overline{B_{1}} \: B_{0}}
\mathrm{D_{6} \: = \: \overline{B_{3}} \: B_{2} \: B_{1} \: \overline{B_{0}}}
\mathrm{D_{7} \: = \: \overline{B_{3}} \: B_{2} \: B_{1} \: B_{0}}
\mathrm{D_{8} \: = \: B_{3} \: \overline{B_{2}} \: \overline{B_{1}} \: \overline{B_{0}}}
\mathrm{D_{9} \: = \: B_{3} \: \overline{B_{2}} \: \overline{B_{1}} \: B_{0}}
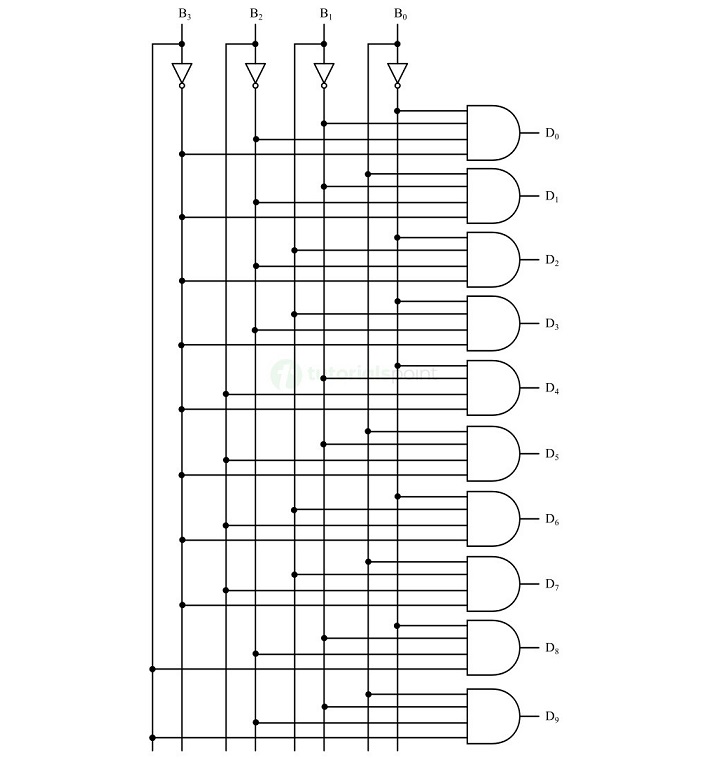
BCD 到十进制转换器的逻辑电路实现如图所示。
