Digital-electronics 简明教程
Maxterm Representation of Boolean Expression
K-Map 或 Karnaugh Map 是一种简化复杂布尔函数或表达式的系统方法。Karnaugh 图(K 图)基本上是一个由一定数量的相邻单元格组成的图或图表。每个单元格表示变量在求和或乘积形式中的特定组合。
The K-Map or Karnaugh Map is a systematic method of simplifying a complex Boolean function or expression. The K-Map is basically a graph or a chart which consists of a certain number of adjacent cells. Each cell represents a particular combination of variables in either sum or product form.
但是,我们可以使用 Karnaugh 图来简化任何数量变量的布尔函数,但对于涉及五个或更多变量的函数来说,这变得很繁琐。在实际应用中,我们通常使用 Karnaugh 图来简化多达六个变量的布尔函数。
However, we can use the K-Map for simplifying a Boolean function in any number of variables, but it becomes tedious for functions involving five or more variables. In actual practice, we usually use K-Map for simplification of Boolean functions in upto six variables.
n 个变量的布尔函数在乘积和(SOP)形式中可能具有 2n 个乘积项的组合,或者在求和积(POS)形式中可能具有 2n 个求和项的组合。
A Boolean function in n variables can have 2n possible combinations of product terms in sum of products (SOP) form, or 2n possible combinations of sum terms in product of sums (POS) form.
因此,对于 2 个变量的布尔函数,Karnaugh 图将具有 22 = 4 个单元格,对于 3 个变量的函数,它将具有 23 = 8 个单元格,依此类推。
Therefore, for a Boolean function in 2 variables, the K-map will have 22 = 4 cells, for a function in 3 variables, it will have 23 = 8 cells, and so on.
布尔函数可以用两种规范或标准形式表示,即 SSOP (Standard Sum of Products) Form and SPOS (Standard Product of Sums) Form 。
A Boolean function can be expressed in two canonical or standard form namely SSOP (Standard Sum of Products) Form and SPOS (Standard Product of Sums) Form.
SSOP 形式是一种布尔函数表示为乘积项和的形式,其中表达式的每个项都包含函数的所有变量,以取反或未取反的形式。SSOP 形式中逻辑表达式的每个乘积项称为 minterm 。
A SSOP form is one in which a Boolean function is expressed as a sum of product terms, where each term of the expression contains all the variables of the function in either complemented or un-complemented form. Each product term of the logic expression in SSOP form is referred to as a minterm.
例如,
For example,
\mathrm{Y \: = \: AB \: + \: \overline{A}B}
这里,Y 是两个变量 A 和 B 的布尔函数。项 AB 和 AB' 是函数的最小项。
Here, Y is a Boolean function in two variables A and B. The terms AB and AB' are the minterms of the function.
在 SPOS 形式中,布尔函数表示为求和项的乘积,其中每个求和项(称为 maxterm )都包含函数的所有变量,以取反或非取反的形式。
In the SPOS form, a Boolean function is expressed as a product of sum terms, where each sum term, called maxterm, contains all the variables of the function in either complemented or non-complemented form.
例如,
For example,
\mathrm{Y \: = \: \lgroup A \: + \: B\rgroup \: .\: \lgroup \overline{A} \: + \: B \rgroup}
这里,Y 是两个变量 A 和 B 的布尔函数,项 (A+B) 和 (A'+B) 是该函数的两个最大项。
Here, Y is a Boolean function in two variables A and B, and the terms (A+B) and (A'+B) are the two maxterms of the function.
这篇文章主要是为了解释如何在 K-map 上用最长乘积范式表示布尔函数。因此,让我们讨论一下最长乘积表示法或在 K-map 上绘制 0。
This article is primarily meant for explaining how to represent a Boolean function in Max Term form on a K-map. So, let us discuss the maxterm representation or plotting zeros on K map.
Plotting Zeros (Maxterm Representation)
正如我们之前讨论过的,标准 POS 形式表达式中的每个和项称为一个最长乘积项。一个最长乘积项用大写字母 M 表示,其下标表示该最长乘积项的十进制标记。
As we already discussed that each sum term in a standard POS form expression is called a maxterm. A maxterm is denoted by the uppercase letter M with a subscript which denotes the decimal designation of that maxterm.
要将一个标准 POS 表达式表示在 K-map 上,需要在表达式中表示的最长乘积项对应的单元格中绘制 0,对于表达式中没有的最长乘积项,则不进行任何条目。
For representing a standard POS expression on to the K-map, zeros are plotted in the cells corresponding to the maxterms which are represented in the expression, and no entries are made in the cells corresponding to the maxterms which are not present in the expression.
现在,为了更好地理解绘制 0 或最长乘积表示法的概念,让我们讨论一些已解决的例子。
Now, for better understanding of the concept of plotting zeros or maxterm representation, let us discuss some solved examples.
Example 1
在 K-Map 上绘制以下 2 个变量布尔表达式。
Plot the following 2 variable Boolean expression on the K-Map.
\mathrm{Y \: = \: \lgroup A \: + \: B \rgroup\lgroup A \: + \: \overline{B} \rgroup\lgroup \overline{A} \:+ \: B \rgroup}
Solution
根据最长乘积项可将给定布尔表达式表示为,
The given Boolean expression in terms of maxterms can be represented as,
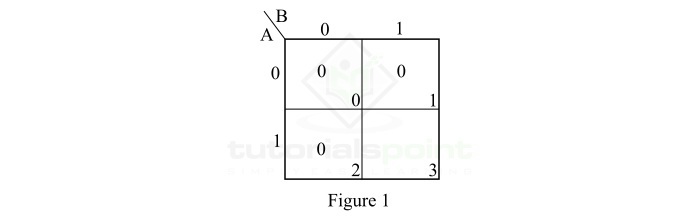
\mathrm{Y \: = \: M_{3} \cdot M_{2} \cdot M_{1} \: = \: \prod M \lgroup 0, \: 1, \: 2 \rgroup}
此函数的最长乘积表示法在 K-map 上的图 1 中展示。
The maxterm representation of this function on the K-map is shown in Figure-1.
Example 2
在 K-map 上绘制以下 3 个变量布尔函数。
Plot the following 3 variables Boolean function on the K-Map.
\mathrm{Y \: = \: \lgroup A \: + \: B \: + \: C \rgroup\lgroup \overline{A} \: + \: \overline{B} \: + \: C\rgroup \lgroup A \: + \: B \: + \: \overline{C}\rgroup\lgroup \overline{A} \: + \: B \: + \: \overline{C} \rgroup \lgroup \overline{A} \: + \: \overline{B} \: + \: \overline{C}\rgroup}
\mathrm{Y \: = \: \lgroup A \: + \: B \: + \: C \rgroup\lgroup \overline{A} \: + \: \overline{B} \: + \: C\rgroup\lgroup A \: + \: B \: + \: \overline{C}\rgroup\lgroup \overline{A} \: + \: B \: + \: \overline{C} \rgroup\lgroup \overline{A} \: + \: \overline{B} \: + \: \overline{C}\rgroup}
Solution
根据最长乘积项可将给定布尔函数表示为,
The given Boolean function in terms of maxterms can be represented as,
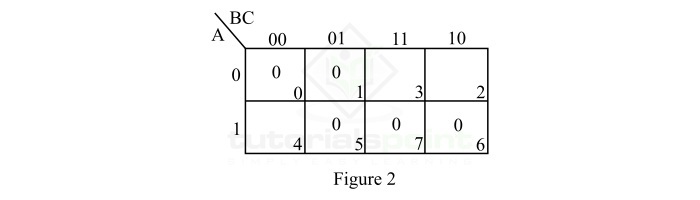
\mathrm{Y \: = \: M_{0} \cdot M_{1}\cdot M_{5} \cdot M_{6} \cdot M_{7} \: = \: \prod M \lgroup 0, \: 1, \: 5, \: 6, \: 7 \rgroup}
此函数的最长乘积表示法在 K-map 上的图 2 中展示。
The maxterm representation of this function on the K-map is shown in Figure 2.
因此,上述就是关于在 K-map 上绘制布尔表达式的 0 或最长乘积表示法的所有内容了。
Hence, this is all about plotting zeros or maxterm representation of Boolean expression on the K-map.
Tutorial Problems
尝试解决以下教程问题以更清楚地理解该概念。
Try to solve the following tutorial problems to understand the concept more clearly.
Q1. 在 K-map 中用最长乘积表示绘制以下布尔表达式。
Q1. Plot the following Boolean expression in maxterm representation on the K-map.
\mathrm{f( A, \: B) \: = \: (A \: + \: B)\cdot(\overline{A} \: + \: B).(\overline{A} \: + \: \overline{B})}
Q2. 在 K-map 中用最长乘积表示绘制以下 3 个变量布尔函数。
Q2. Plot the following 3 variable Boolean function in maxterm representation on the K map.
\mathrm{f(A, \: B, \: C) \: = \: (A \: + \: B \: + \: \overline{C})\cdot(A \: + \: \overline{B} \: + \: C)\cdot( \overline{A} \: + \: \overline{B} \: + \: C)\cdot(\overline{A} \: + \: B \: + \: \overline{C})}