Digital-electronics 简明教程
Digital Electronics - K-Map Minimization
What is Karnaugh Map?
在实现数字电子系统中,化简布尔表达式是最关键的步骤之一,因为它可以降低硬件复杂性和生产成本。有许多工具和方法可用于化简复杂的布尔表达式。K 映射或 Karnaugh 映射就是其中一种化简方法。K 映射是 Maurice Karnaugh 在 1953 年开发的。这是一种用于化简布尔表达式的可视化或图形化方法。
In realization of digital electronic systems, the simplification of Boolean expressions is one of the most crucial steps because it reduces the hardware complexity and cost of production. There are several tools and methods available for simplifying complex Boolean expression. K-Map or Karnaugh Map is one of such simplification methods. K-Map was developed by Maurice Karnaugh in the year of 1953. It is a visual or graphical method used to simplify the Boolean expressions.
当布尔表达式中的变量数小于或等于 4 时,K 映射是最有效的化简工具之一。然而,对于五个、六个或更多个变量,K 映射就会变得相当困难。
K-Map is one of the most efficient simplification tools when the number of variables in the Boolean expression are less than or equal to four. However, for five, six, and more variables, the K-Map becomes quite difficult.
K 映射或 Karnaugh 映射利用二维表格来化简布尔函数。随着布尔函数中变量数的增加,此表格的大小会显著增加。
The K-Map or Karnaugh map makes the use of two dimensional table for simplification of the Boolean functions. The size of this table increases considerably with the increase in the number of variables in the Boolean functions.
图 1 中显示了两个变量、三个变量和四个变量的一些典型 K 映射示例。
Some typical examples of K-Map of two variable, three variable, and four variables are shown in Figure-1.
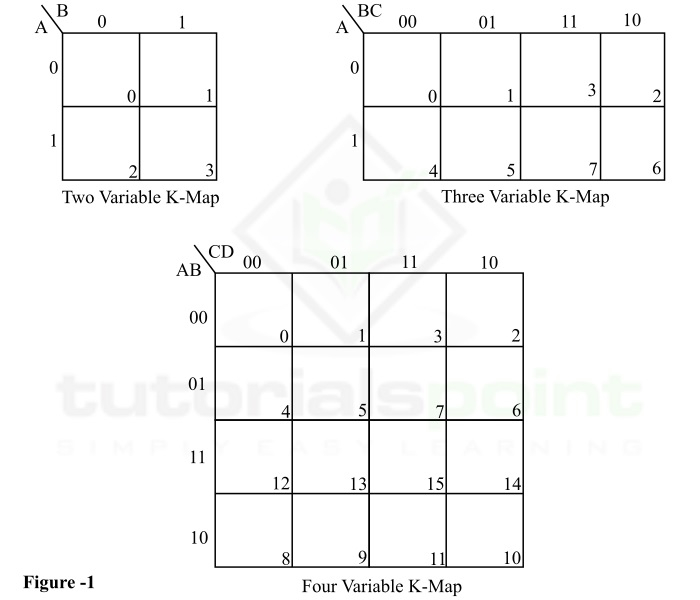
从图 1 中可以明显看出,Karnaugh 映射中的方块或单元格数取决于表达式中变量的数目。
From Figure-1, it is clear that the number of squares or cells in the Karnaugh map depends on the number of variables in the expression.
如果给定布尔函数中的变量数为 n,那么相应的 Karnaugh 映射 (K 映射) 将有 2n 个方块或单元格。例如,如果布尔函数中的变量数为 3,那么相应的 K 映射将有 8 (= 23) 个单元格。
If n is the number of variables in the given Boolean function, then the corresponding Karnaugh map (K-Map) will have 2n squares or cells. For examples, if the number of variables in the Boolean function is 3, then the corresponding K-Map will have 8 (= 23) cells.
Structure of Karnaugh Map
所有卡诺图或K映射均具有广义的类似结构,如图 1 所示。一个典型的 K 映射具有一定的单元表。此表的左上角表示一组变量 A、B、C、D。这些变量基本上是逻辑表达式中涉及的输入变量,需要简化该逻辑表达式。
All the Karnaugh maps or K-Maps have a generalized similar structure as shown in Figure-1. A typical K-Map has a table of certain cells. On the top-left corner of this table, a set of variables are represented as A, B, C, D. These variables are basically the input variables involved in the logical expression that requires to be simplified.
沿着各个变量的侧面(即在表的顶部和左侧)以二进制形式表示这些输入变量的值。
The values of these inputs variables in binary form are represented along their respective sides, i.e., on the top and left of the table.
从上述示例中,可以观察到,K 映射顶部和左侧的二进制数不是按正常的二进制顺序排列,而是按格雷码排列。格雷码用于确保两个物理相邻的单元实际上是相邻的。这让我们在最小化布尔表达式期间更容易分组。
From the above examples, it can be observed that the binary numbers along the top and left of the K-Map are not in their normal binary order, instead they are in the gray code. The Gray code is used to ensure that the two physically adjacent cells are actually adjacent. This makes the process of grouping easier during minimization of the Boolean expression.
为了让 K 映射更容易阅读,每个 K 映射的单元会分配一个十进制数,该数字表示在单元的右下角。例如,在三变量 K 映射(图 1)中,K 映射的第二个单元表示位模式 001,因此该单元用其十进制等效值 1 表示。
For providing simplicity in reading the K-Map, each cell of the K-Map is assigned a decimal number represented at the bottom-right corner of the cell. For example, in the three variable K-map (figure-1), the second cell of the K-Map represents a bit pattern 001, hence this cell is represented by its decimal equivalent 1.
K-Map Simplification
K 映射或卡诺图简化过程开始于将变量的值(以其 SOP(乘积和)形式或 POS(和之积)形式)输入到右侧 K 映射单元中。之后,我们需要对最大数量的 1(对于 SOP 形式)或最大数量的 0(对于 POS 形式)进行分组。这些组中的每一个都必须是 2 的幂,并且必须仅按递减顺序进行。
The procedure of K-Map or Karnaugh map simplification is started with the entering the values of the variables, either in their SOP (Sum of Products) form or in POS (Product of Sums) form, in the right K-map cells. After that we need to group the maximum number of 1s (in the case of SOP form) or the maximum number of 0s (in the case of POS form). Each of these groups must be in powers of 2 and must be carried on in decreasing order only.
完成分组后,每个组必须根据与其关联的行和列上的公共二进制值对应的输入变量组合来表达。最后,所有组合表达布尔函数的输出表达式。
Once the grouping is done, each group has to be expressed in terms of combinations of input variables which are corresponding to the common binary values along the associated rows and columns. At last, all the combinations express the output expression of the Boolean function.
Advantages of Karnaugh Map
卡诺图有以下重要优点:
The following are the important advantages of the Karnaugh map −
-
For simplifying Boolean expression, the K-map does not require the knowledge of theorems of Boolean algebra.
-
Karnaugh map involves less number of steps in simplification process of logical expressions as compared to other simplification techniques.
Limitations of Karnaugh Map
卡诺图的主要限制如下:
The following are the major limitations of the Karnaugh map −
-
The most significant limitation of the Karnaugh map is that it is only efficient when the Boolean expression has less number of variables. It becomes quite complicated with the higher number of variables in the logical expression.
-
The simplification of a Boolean function having more than or equal to five variables using K-Map is quite complex.
-
It is very difficult to get equations correct with more than 5 variables using the K-map.
Conclusion
卡诺图或 K 映射是用于简化多达 4 个变量的布尔表达式的有效工具。这是一种简化逻辑表达式的简单方法,因为它不使用布尔代数定理。K 映射的另一个优点是它是一种视觉化的简化方法。但是,当逻辑表达式中的变量等于或超过 5 时,K 映射会变得复杂且效率低下。
The Karnaugh map or K-Map is an efficient tool for simplifying Boolean expression up to 4 variables. It is an easy method for simplification of logic expression because it does not make the use of Boolean algebra theorems. Another advantage of K-Map is that it is a visual method of simplification. However, the K-map becomes complex and inefficient when the variables in the logical expression are equal to or more than 5.