Digital-electronics 简明教程

XNOR Gate in Digital Electronics

一个 XNOR gate 是一种派生逻辑门类型，是 XOR 门和 NOT 门的组合。因此，它生成一个“取反 XOR”输出。

An XNOR gate is a type of derived logic gate which is a combination of an XOR gate and a NOT gate. Hence, it produces a "NOTed XOR" output.

在本章中，我们将解释 XNOR 逻辑门的基本原理、其工作原理、电路图和应用。我们从 XNOR 门的基本定义开始。

In this chapter, we will explain the basic theory of XNOR logic gate, its working, circuit diagrams, and applications. So, let’s start with the basic definition of XNOR gate.

What is XNOR Gate?

XNOR 门是一种具有两个输入和一个输出的逻辑门。

The XNOR gate is a logic gate that has two inputs and one output.

只有在 XNOR 门的两个输入都相同时，即两个输入都高电平或都低电平时，其输出才高电平。如果输入不同，即一个高电平而另一个低电平，则输出低电平或逻辑 0。

The output of the XNOR gate is high, only when both of its inputs same, i.e., either both inputs are high or both inputs are low. If the inputs are dissimilar, i.e., one is high and the other low, the output is low or logic 0.

由于 XNOR 门在其两个输入都类似时产生高电平输出，因此它也被称为 equality detector 。

Since the XNOR gate produces a high output when both its inputs are similar, it is also known as an equality detector.

XNOR 门也被称为 Exclusive-NOR 或 Ex-NOR gate 。

The XNOR gate is also known as Exclusive-NOR or Ex-NOR gate.

实际上，XNOR 门是两个逻辑门的组合，即 XOR 门和 NOT 门。因此，

Actually, the XNOR gate is a combination of two logic gates namely, XOR gate and NOT gate. Therefore,

XNOR Gate = XOR Gate + NOT Gate

重要的是记住，不存在具有三个或更多输入的 XNOR 门。要获得具有两个以上输入的 XNOR 门，我们需要将多个两个输入的 XNOR 门组合在一起。

It is important remember that there is no such thing like an XNOR gate with three or more inputs. To obtain an XNOR gate with inputs more than two, we combine multiple two-input XNOR gates together.

Logic Symbol of XNOR Gate

两个输入 XNOR 门的逻辑符号如下图所示。

The logic symbol for a two input XNOR gate is shown in the following figure.

右侧的气泡表示 NOT 运算。变量 A 和 B 表示输入线，而 Y 表示输出线。

The bubble on the right-end represents the NOT operation. The variables A and B represent the input lines while Y represents the output line.

Truth Table of XNOR Gate

异或门真值表提供了有关异或门运算和输入与输出之间关系的信息。

The truth table of an XNOR gate provides information about the operation and relationship between inputs and output of it.

双输入异或门的真值表如下所示：

The truth table of a two-input XNOR gate is given below −

Input	Output
A	B
Y	0
0	1
0	1
0	1
0	0
1	1

从这个真值表中可以看出，当异或门的两个输入相同时，即 0 和 0 或 1 和 1，异或门产生高电平或逻辑 1 输出。否则，它会产生低电平或逻辑 0 输出。

From this truth table, it can be observed that the XNOR gate produces a high or logic 1 output when both of its inputs are same i.e., 0 and 0 or 1 and 1. Otherwise, it gives a low or logic 0 output.

Boolean Expression of XNOR Gate

布尔表达式是一个逻辑函数，用数学形式描述了异或门的输入与输出之间的关系。

The Boolean expression is a logical function that describes the relationship between inputs and output of an XNOR gate mathematically.

双输入异或门的布尔表达式如下所示：

The Boolean expression of a two-input XNOR gate is given below −

\mathrm{Y \: = \: A \: \odot \: B}

这也可用以下方式表示：

This can also be expressed as,

\mathrm{Y \: = \: AB \: + \: \bar{AB}}

这里，A 和 B 是输入变量，而 Y 是输出变量。

Here, A and B are input variables while Y is the output variable.

Working of XNOR Gate

下文解释了用于不同输入组合的双输入异或门的运算：

The operation of a two-input XNOR gate for different input combinations is explained below −

If A = 0 and B = 0, the output of the XNOR gate is Y = 1.
If A = 0 and B = 1, the output of the XNOR gate is Y = 0.
If A = 1 and B = 0, the output of the XNOR gate is Y = 0.
If A = 1 and B = 1, the output of the XNOR gate is Y = 1.

因此，我们可以看到，对于相似的输入，输出为高电平或逻辑 1。对于不相似的输入，输出为低电平或逻辑 0。

Hence, we can see that the output is high or logic 1 for similar inputs. It is low or logic 0 for dissimilar inputs.

XNOR Gate using Switches

我们可以借助两个开关、一个电池和一个灯来实现异或门逻辑。

We can realize the XNOR gate logic with the help of two switches, a battery, and a lamp.

这是表示异或逻辑门的电路图。

Here is the electrical circuit representing the XNOR logic gate.

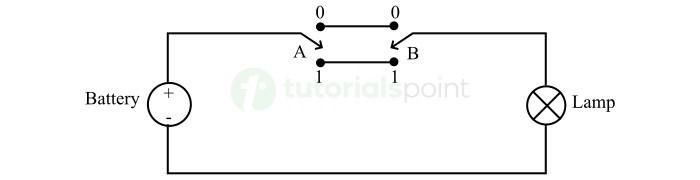
在这个电路中，当开关 A 和 B 都处于相同电平时，即 0 和 0 或 1 和 1，电流可以通过灯泡流动形成一个闭合回路。这会使灯泡亮起，表示高电平或逻辑 1 输出。

In this circuit, when both switches A and B are at same level i.e., at 0 and 0 or 1 and 1. There is a closed path for the current to flow through the lamp. This turns on the lamp and represents the high or logic 1 output.

如果开关处于不同电平，也就是说一个开关处于电平 0，另一个开关处于电平 1。电池和灯之间没有完整的路径。因此，灯不会发光，并且表示低电平或逻辑 0 输出。

If the switches are at different levels i.e., one is at level 0 and the other is at level 1. There is no complete path between the battery and lamp. Hence, the lamp will not glow and represent the low or logic 0 output.

因此，上面所示的开关电路实现了异或非逻辑运算。

Hence, the above shown switching circuit implements the XNOR logic operation.

XNOR Gate as an Inverter

异或非门可以用作反相器。如果我们将异或非门的一条输入线连接到低电平或逻辑 0 信号，并将输入信号应用于另一条输入线。然后，异或非门的输出将是所应用输入的补数。

The XNOR gate can operate as an inverter. If we connect one of the input lines of the XNOR gate at low or logic 0 signal and we apply the input signal to another input line. Then, the output of the XNOR gate will be the complement of the input applied.

异或非门用作反相器的逻辑电路如下图所示。

The logic circuit of an XNOR gate working as an inverter is depicted in the following figure.

我们还可以借助它的布尔表达式来解释这个运算，如下所示。

We can also explain this operation with the help of its Boolean expression as below.

\mathrm{Y \: = \: AB \: + \: \bar{AB}}

如果 B 设置为逻辑 0，则

If B is set at logic 0, then

Y := A·0 : + : ¬A·1 := ¬A

\mathrm{Y \: = \: A\cdot0 \: + \: \bar{A}\cdot1 \: = \: \bar{A}}

因此，如果一个输入异或非门连接到逻辑 0，则该门将用作反相器。

Hence, if one input XNOR gate is tied to logic 0, then the gate will work as an inverter.

XNOR Gate as a Buffer

异或非门也可以用作缓冲器。如果我们把异或非门的一个输入连接到逻辑 1，并将输入信号应用到另一个输入线。异或非门的输出将与所应用的输入相同，即异或非门将用作缓冲器。

The XNOR gate can also operate as a buffer. If we connect of one of the inputs of the XNOR gate to logic 1 and the input signal is applied to another input line. The output of the XNOR gate will be same as the input applied, i.e., the XNOR gate will work as a buffer.

异或非门用作缓冲器如下图所示。

The XNOR gate working as a buffer is shown in the following figure.

从逻辑上讲，我们可以通过布尔表达式证明该运算，如下所示。

Logically, we can prove this operation through its Boolean expression as below.

\mathrm{Y \: = \: AB \: + \: \bar{AB}}

如果 B 设置为逻辑 1，则

If B is set at logic 1, then

Y := A·1 : + : ¬A·0 := A

\mathrm{Y \: = \: A\cdot1 \: + \: \bar{A}\cdot0 \: = \: A}

因此，一个输入设置为逻辑 1 的异或非门充当缓冲器。

Thus, an XNOR gate with one input set to logic 1 acts as a buffer.

Applications of XNOR Gate

异或非门广泛用于多种数字电路和系统中。异或非门的一些主要应用如下 -

The XNOR gate is widely used in numerous digital circuits and systems. Some of the key applications of XNOR gate are given below −

XNOR gate is used in digital communication systems to detect errors that occurred during data transmission.
XNOR gate acts as an equality detector. Thus, it is also used to compare binary data or signals.
XNOR gate is also used to design digital gaming systems and logic puzzles.

Conclusion

总之，异或非门或异或非门是一种用于各种数字电子应用中的逻辑门。它是一个二输入逻辑门。

In conclusion, the XNOR gate or Exclusive NOR gate is a logic gate used in various digital electronic applications. It is a two-input logic gate.

与或门独有的等值检测功能广泛应用于数字信号比较和数据传输错误校验中。

The unique functionality of the XNOR gate of equality detection is widely used in digital signal comparison and data transmission error checking.

在本章中，我们阐述了与或门的理论基础和工作原理，以及它的关键应用。

In this chapter, we explained the basic theory and working of the XNOR gate along with its key applications.