Digital-electronics 简明教程
Digital Electronics - Octal Arithmetic
What is Octal Arithmetic?
在数字电子领域中,八进制数字被广泛地用于系统设计、编码、解码等。八进制算术可以被定义为提供用于操纵八进制数字的一组规则和运算符的数学。换句话说,一个使用八进制数字进行数值计算的数学系统被称为八进制算术。
In digital electronics, octal numbers are widely used in system designing, encoding, decoding, etc. Octal arithmetic can be defined as the mathematics that provides a set of rules and operators to manipulate octal numbers. In other words, a mathematical system of numerical calculations that utilizes octal numbers is referred to as octal arithmetic.
在八进制算术中,我们可以执行以下四个基本算术运算:
In octal arithmetic, we can perform the following four basic arithmetic operations −
-
Octal Addition
-
Octal Subtraction
-
Octal Multiplication
-
Octal Division
在数字电子系统中,八进制数字以更简洁的形式用于表示二进制信息和数据,因为一个八进制数字可以表示一组三进制数字或一位。因此,了解八进制算术在数字电子学的学习中很重要。
In digital electronic systems, octal numbers are used to represent binary information and data in a more compact form, as an octal digit can represent a group three binary digits or bits. Therefore, the understanding of octal arithmetic is important in the study of digital electronics.
让我们借助示例详细地逐一讨论这四个八进制算术运算。
Let us discuss each of the four octal arithmetic operations one-by-one in detail with the help of examples.
Octal Addition
在八进制算术中,八进制加法是用于将两个或多个八进制数字相加以得到其和的基本算术运算之一。八进制加法类似于十进制加法。但是,在八进制加法的情况下,当和等于或大于 8 时,会产生一个进位传递到下一列。
In octal arithmetic, octal addition is one of the basic arithmetic operations used to add two or more octal numbers to produce their sum. Octal addition is similar to decimal addition. But, in the case of octal addition, a carry is generated to pass over to the next column when the sum is equal to or greater than 8.
让我们看一些已解决的示例来理解八进制加法的过程。
Let us see some solved examples to understand the process of octal addition.
Explanation
相加最右列的八进制数字:5 + 2 = 7。将数字 7 写下来作为结果。
Add the octal digits in the rightmost column: 5 + 2 = 7. Write down the digit 7 as result.
移到第二列并相加八进制数字 1 和 2:1 + 2 = 3。将数字 3 写下来作为结果。
Move to the second column and add the octal digits 1 and 2: 1 + 2 = 3. Write down the digit 3 as result.
移到下一列并相加第三列的八进制数字:3 + 2 = 5。将数字 5 写下来作为结果。
Move to the next column and add the octal digits in the third column: 3 + 2 = 5. Write down the digit 5 as result.
因此,315 和 222 的八进制加法的最终结果是 537。
Hence, the final result of octal addition of 315 and 222 is 537.
Explanation
相加最右列的八进制数字:2 + 6 = (10)8。因此,将最后一位数字(0)写下来作为结果,然后将 1 进位到下一列。
Add the octal digits in rightmost column: 2 + 6 = (10)8. Thus, write down the last digit (0) as the result and carry over the 1 to the next column.
移动到第二列并添加从上一步骤中进位的八进制数字:7 + 1 + 1 = (11)8。将最后一位数 (1) 写为结果,并将左边的 1 进位到下一列。
Move to the second column and add the octal digits including the carry-over from the previous step: 7 + 1 + 1 = (11)8. Write the last digit (1) as the result and carry over left 1 to the next column.
移动到第三列并添加八进制数字以及来自上一步骤的进位:3 + 7 + 1 = 13。没有要添加的数字了。因此,写下结果。
Move to the third column and add the octal digits along with the carry from the previous step: 3 + 7 + 1 = 13. No digits left to add. Thus, write down the result.
因此,八进制加法的最终结果是 1310。
Hence, the final result of the octal addition is 1310.
Octal Subtraction
八进制减法是针对八进制数执行的另一项基本算术运算。它用于找出两个八进制数之间的差值。
Octal subtraction is another basic arithmetic operation performed on octal numbers. It is used to find the difference between two octal numbers.
令八进制减法为 (x)8 - (y)8,如果数字 x 小于数字 y,则从下一个高位位置借用 1 来执行八进制减法。
Let an octal subtraction as (x)8 - (y)8, if the digit x is smaller than the digit y, a borrow 1 from the next higher order position is taken to perform the octal subtraction.
让我们看一些已解决的示例来了解八进制减法。
Let us see some solved examples to understand the octal subtraction.
Explanation
从最右侧列中的数字开始减去:5 – 3 = 2。将数字 2 作为结果写下。
Start subtracting from the digits in the rightmost column: 5 – 3 = 2. Write down the digit 2 as result.
移动到下一列并减去数字:2 – 1 = 1。将数字作为结果写下。
Move to the next column and subtract the digits: 2 – 1 = 1. Write down the digit as result.
移动到下一列并减去八进制数字:3 – 2 = 1。将数字 1 作为结果写下。
Move to the next column and subtract the octal digits: 3 – 2 = 1. Write down the digit 1 as result.
因此,给定的八进制减法的最终结果是 (112)8。
Thus, the final result of the given octal subtraction is (112)8.
Solution
数字 3178 和 1258 的八进制减法如下解释−
The octal subtraction of numbers 3178 and 1258 is explained below −

Explanation
减去最右侧数字:7 – 5 = 2。将数字 2 作为结果写下。
Subtract rightmost digits: 7 – 5 = 2. Write down the digit 2 as result.
移动到第二列并减去数字:1 – 2。由于 1 小于 2,因此从下一个高位数字借用 1 来使它变为 11。因此,八进制减法为 11 – 2 = 7。将八进制数字 7 作为结果写下。
Move to the second column and subtract digits: 1 – 2. Since 1 is less than 2, a borrow 1 from the next higher digit is taken that makes it 11. Thus, the octal subtraction is 11 – 2 = 7. Write down the octal digit 7 as result.
移动到最左侧列并减去数字:2 – 1 = 1。将数字 1 作为结果写下。
Move to the leftmost column and subtract the digits: 2 – 1 = 1. Write down the digit 1 as result.
因此,减法的最终结果是 (172)8。
Thus, the final result of the subtraction is (172)8.
Octal Multiplication
八进制乘法是对八进制数执行的第三个基本算术运算。它用于找到两个八进制数的乘积。
Octal multiplication is the third basic arithmetic operation performed on octal numbers. It is used find the product of two octal numbers.
八进制乘法通过对一个八进制数字的每一位分别乘以另一个八进制数字的每一位来进行。最终结果通过对乘法的所有部分积求和得到。
The octal multiplication is performed by multiplying each digit of one octal number by each digit of another octal number. The final result is obtained by summing up all the partial products of the multiplication.
下面的数字示例展示了执行八进制乘法的方法。
The following numerical examples demonstrate the method of performing octal multiplication.
Explanation
将八进制数字 5 乘以八进制数字 375 的每一位。写下乘法的结果以得到最终乘积 (2361)8。
Multiply the octal digit 5 by each digit of the octal number 375. Write down the results of multiplication to get the final product that is (2361)8.
Explanation
将第二个八进制数字 25 的最右边位数 (5)8 乘以第一个八进制数字 624 的每一位,并写下部分积。
Multiply the rightmost digit (5)8 of the second octal number 25 by each digit of the first octal number 624 and write down the partial products.
移到八进制数字 25 的下一个位数 (2)8,并将其乘以八进制数字 624 的每一位。向左移一位并写下部分积。
Move to the next digit (2)8 of the octal number 25 and multiply it by each digit of the octal number 624. Shift one position to the left and write down the partial product.
添加所有部分积以获得最终结果,即 (20444)8。
Add all the partial products to obtain the final result, that is (20444)8.
Octal Division
八进制除法是一种基本算术运算,它可以对八进制数字执行以找到商数和余数。
Octal division is one of the basic arithmetic operations that can be performed on octal numbers to find their quotient and remainder.
八进制除法的逐步过程如下所述 −
The step-by-step procedure of octal division is described below −
Step 1 − 从将被除数的最左位数除以除数开始。
Step 1 − Start by dividing the leftmost digits of the dividend by the divisor.
Step 2 − 将所得商乘以除数,然后从被除数中减去乘积。
Step 2 − Multiply the quotient obtained by the divisor and subtract the product from the dividend.
Step 3 − 将被除数的下一个八进制位数降下来,并重复以上两个步骤,直到使用被除数中的所有位数。
Step 3 − Bring down the next octal digits of the dividend and repeat the above two steps until all the digits in the dividend are used.
让我们通过一些已解决的示例理解八进制数字的除法。
Let us understand the division of octal numbers through some solved examples.
Solution
给定数字的八进制除法如下所示 −
The octal division of given numbers is shown below −
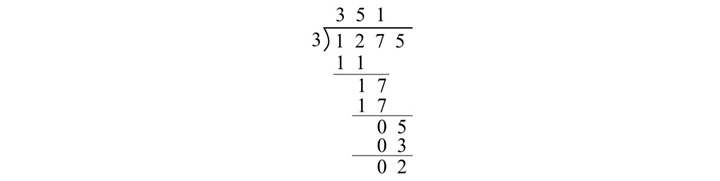
在这个示例中,八进制数字 (1275)8 除以 (3)8 得出商数 (351)8 和余数 (2)8。
In this example, the division of octal number (1275)8 by (3)8 gives (351)8 as quotient and (2)8 as remainder.
让我们看另一个示例以更好地理解八进制除法。
Let us take another example for a better understanding of octal division.
Solution
下面描述给定数字的八进制除法。
The octal division of given numbers is described below −
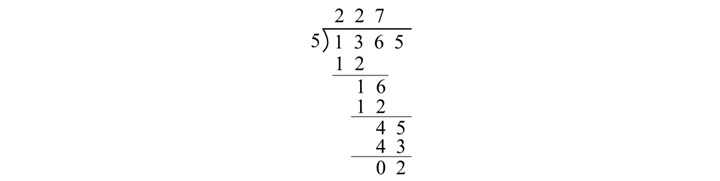
在八进制除法的这个示例中,商为 (227)8,余数为 (2)8。
In this example of octal division, the quotient is (227)8 and the remainder is (2)8.
我们还可以通过将它们转换为二进制形式来执行八进制算术运算。众所周知,一个八进制数字可以用一组 3 个二进制数字(或位)表示。
We can also perform octal arithmetic operations by converting them to binary form. As we know, an octal digit can be represented by a group of 3 binary digits or bits.
下表给出了每个八进制数字的二进制表示形式。
The binary representation of each octal digit is given in the following table −
Octal Digit |
3-Bit Binary |
0 |
000 |
1 |
001 |
2 |
010 |
3 |
011 |
4 |
100 |
5 |
101 |
6 |
110 |
7 |
111 |
让我们看一些示例来学习如何通过二进制转换来进行八进制算术运算。
Let us see some examples to learn the octal arithmetic operations through binary conversion.
Octal Addition through Binary Conversion
可以通过下列步骤用二进制转换对两个八进制数进行加法:
The addition of two octal numbers through binary conversion can be performed as per the following steps −
Step 1 − 将给定的八进制数转换为它们的二进制等效数。
Step 1 − Convert the given octal number to their binary equivalent.
Step 2 − 加上获得的二进制数。
Step 2 − Add the obtained binary numbers.
Step 3 − 将最终结果转换回八进制格式。
Step 3 − Convert final result back to the octal format.
Solution
将给定的八进制数转换为其二进制等效数。
Converting the given octal numbers to their binary equivalents.
(75)8 = (111 101)2
(14)8 = (001 100)2
以二进制格式添加八进制数,
Adding the octal numbers in their binary format,

将二进制数转换为八进制数以获得最终结果,
Converting the sum from binary to octal to obtain the final result,
(001 001 001)2 = (111)8
Octal Subtraction through Binary Conversion
要通过二进制转换对两个数字进行八进制减法,我们首先将它们转换为其二进制等效形式,然后根据二进制减法的规则执行减法,最后将最终结果转换回八进制数系统。
To perform octal subtraction of two numbers through binary conversion, we first convert them to their binary equivalent, then perform subtraction according to the rules of binary subtraction, and finally convert the final result back to the octal number system.
这是一个示例,演示如何通过二进制转换执行八进制减法。
Here is an example that demonstrates how you can perform octal subtraction through binary conversion.
Octal Multiplication Through Binary Conversion
就像加法和减法一样,我们也可以通过将八进制数转换为二进制数来执行八进制数的乘法。以下示例演示如何通过二进制转换执行八进制运算。
Just like addition and subtraction, we can also perform the multiplication of octal numbers by converting them into their equivalent binary. The following example demonstrates how you can perform octal multiplication through binary conversion.
Octal Division through Binary Conversion
通过二进制转换执行八进制除法,我们首先将给定的八进制数转换为其等价的二进制数,然后根据二进制除法的规则执行其除法,最后将结果转换回八进制形式。
To perform octal division through binary conversion, we first convert the given octal number to their equivalent binary, then perform their division as per the rules of binary division, and finally convert the result back to the octal form.
以下示例说明了如何通过二进制转换执行八进制除法。
The following example explains how you can perform octal division through binary conversion.
Solution
将给定的八进制数转换为其二进制等价数,
Converting the given octal numbers to their binary equivalents,
(547)8 = (101 100 111)2
(5)8 = (101)2
根据二进制除法运算规则执行二进制除法,
Performing binary division as per the rules of binary division arithmetic,
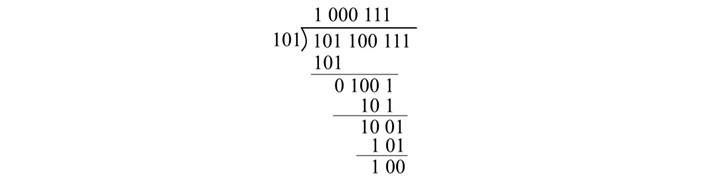
将二进制结果转换回八进制格式,
Converting the binary result back to the octal format,
商 = (1 000 111)2 = (107)8
Quotient = (1 000 111)2 = (107)8
余数 = (100)2 = (4)8
Remainder = (100)2 = (4)8
Conclusion
在本章中,我们解释了各种算术运算,例如八进制数的加法、减法、乘法和除法。
In this chapter, we explained various arithmetic operations such as addition, subtraction, multiplication and division of octal numbers.
我们还介绍了八进制算术运算的二进制方法,在这种方法中,我们首先将给定的八进制数转换为其二进制等价物,然后执行算术运算,最后将二进制结果转换回八进制格式。
We also covered the binary method of octal arithmetic operations in which we first convert the given octal numbers to their binary equivalent, and then perform the arithmetic operations, and finally convert the binary result back to the octal format.






