Digital-electronics 简明教程
5 Variable K-Map in Digital Electronics
K-Map 或 Karnaugh Map 是一种简化技术,用于最小化给定的复杂布尔函数。卡诺图或卡诺图是一种图形或图表,由相邻单元格的排列组成,卡诺图中的每个单元格在求和或乘积形式中都表示变量的特定组合。卡诺图可用于简化涉及任意数量变量的布尔函数。但是,对于涉及五个或更多变量的表达式,使用卡诺图简化布尔函数变得非常复杂。因此,在实际应用中,卡诺图被限制在六个变量。
K-Map or Karnaugh Map is a simplification technique used to minimize a given complex Boolean function. K-Map or Karnaugh Map is a graph or chart which is composed of an arrangement of adjacent cells, where each cell of the K-Map represents a particular combination of variables in either sum or product form. The K-map can be used to simplify Boolean functions involving any number of variables. But, the simplification of a Boolean function using K-map becomes very complex for expressions involving five or more variables. Therefore, in actual practice, the K-map is limited to six variables.
卡诺图中单元格的数量取决于给定布尔函数中变量的数量。卡诺图将有 2n 个单元格或方块,其中 n 是布尔表达式中变量的数量。因此,对于一个二元变量函数,卡诺图将有 22 = 4 个单元格;对于一个三元变量布尔函数,卡诺图将有 23 = 8 个单元格;对于一个四元变量布尔函数,卡诺图将有 24 = 16 个单元格,以此类推。
The number of cells in a K-map depends upon the number of variables in the given Boolean function. A K-map will have 2n cells or squares, where n is the number of variables in the Boolean expression. Therefore, for a two variable function, the K-map will have 22 = 4 cells, for a three variable Boolean function, the K-map will have 23 = 8 cells, and for four variable Boolean function, the K-map will have 24 = 16 cells, and so on.
这里,我们将讨论五元变量卡诺图,并将它用于简化五个变量中的布尔函数。因此,我们从介绍五元变量卡诺图开始。
Here, we will discuss five variable K-Map and will use it to simplify Boolean functions in 5 variables. So let’s start with the introduction of 5 variable K-map.
Five Variable K-Map
五元变量卡诺图用于将一个五元变量布尔表达式最小化为其约简形式。以下是一个五元变量卡诺图的重要特征:
A five variable K-map is used to minimize a 5-variable Boolean expression to its reduced form. The following are the important characteristics of a 5 variable K-map −
一个五元变量卡诺图有 32(25)个单元格或方块,卡诺图中的每个单元格都表示布尔表达式的最简项或最繁项。
A five variable K-map have 32 (25) cells or squares, and each cell of the K-map represents either a minterm or a maxterm of the Boolean expression.
如果给定的布尔函数以 SOP(乘积和)形式表示,则五元变量布尔函数的最简项表示为 m0、m1、m2、m3……m31,其中,m0 对应于 $\mathrm{\lgroup \overline{A} \: \overline{B} \: \overline{C} \: \overline{D} \: \overline{E} \rgroup}$,m1 对应于 $\mathrm{\lgroup \overline{A} \: \overline{B} \: \overline{C} \: \overline{D} E \rgroup}$,… 并且 m31 对应于 $\mathrm{\lgroup ABCDE \rgroup}$。
If the given Boolean function is expressed in SOP (Sum of Products) form, then the minterms of five variables Boolean function are designated as m0,m1,m2,m3 … m31. Where, m0 is corresponding to $\mathrm{\lgroup \overline{A} \: \overline{B} \: \overline{C} \: \overline{D} \: \overline{E} \rgroup}$, m1 is corresponding to $\mathrm{\lgroup \overline{A} \: \overline{B} \: \overline{C} \: \overline{D} E \rgroup}$,… and m31 is corresponding to $\mathrm{\lgroup ABCDE \rgroup}$.
另一方面,如果五元变量布尔函数以 POS(和积)形式表示,则该函数的最繁项表示为 M0、M1、M2、… M31。
On the other hand, if the 5 variable Boolean function is expressed in POS (Product of Sums) form, then the maxterms of the function are designated as M0, M1, M2,… M31.
其中,M0 表示
Where, M0 represents
\mathrm{\lgroup A \: + \: B \: + \: C \: + \: D \: + \: E \rgroup}
M1 表示
M1 represents
\mathrm{\lgroup A \: + \: B \: + \: C \: + \: D \: + \: \overline{E} \rgroup}
M31 表示
M31 represents
\mathrm{\lgroup \overline{A} \: + \: \overline{B} \: + \: \overline{C} \: + \: \overline{D} \: + \: \overline{E} \rgroup}。
\mathrm{\lgroup \overline{A} \: + \: \overline{B} \: + \: \overline{C} \: + \: \overline{D} \: + \: \overline{E} \rgroup}.
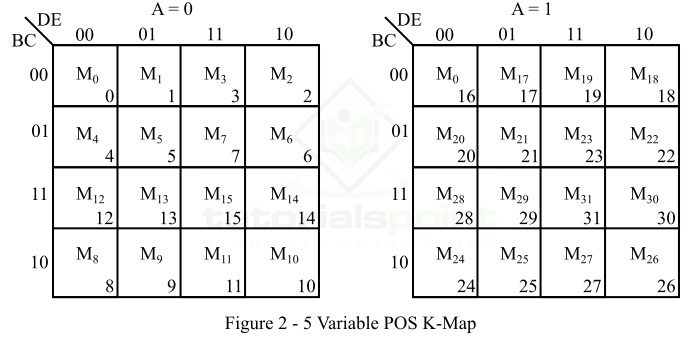
五元变量卡诺图的 32 个单元格被分成两个 16 个单元格的块,它们并排排列。左块表示从 m0 到 m15(或 M0 到 M15)的最简项(或最繁项)。在左块中,第一个变量(让它为 A)为 0。右块表示从 m16 到 m31(或 M16 到 M31)的最简项(或最繁项),此块中的 A 为 1。
The 32 cells of the five variable K-map are divided into two blocks of 16 cells each, which are arranged side by side. The left block represents minterms (or maxterms) from m0 to m15 (or M0 to M15. Wheck, thck, th). In the left block, the first variable (let A) is a 0. The right block represents minterms (or maxterms) from m16 to m31 (or M16 to M31), in this block A is a 1.
在五元变量卡诺图中,我们可以通过用这两个块来形成 2 平方块、4 平方块、8 平方块、16 平方块或 32 平方块。此外,当一个块叠加在另一个块的顶部时,认为这些块在这些块中相邻。
In the five variable K-map, we can form 2-squares, 4-squares, 8-squares, 16-squares, or 32-squares by involving its two blocks. Also, squares are considered adjacent in these two blocks, when one block superimposes on the top of another.
图 1 中显示了一个五元变量 SOP 卡诺图。
A five variable SOP K-map is shown in Figure 1.

图 2 中表示了一个五变量 POS K 图。
A five variable POS K-map is represented in Figure 2.
现在,让我们讨论一些已解决的示例以理解五变量 K 图在以 SOP 形式或 POS 形式约减给定五变量布尔函数中的应用。
Now, let us discuss some solved examples to understand the application of a 5 variable K map in reducing a given 5-variable Boolean function in either SOP form or POS form.
Example 1
使用五变量 K 图,以 SOP 形式约减以下五变量布尔函数。
Reduce the following 5 variable Boolean function in SOP form using the five variable K map.
\mathrm{f \lgroup A,B,C,D,E \rgroup \: = \: \sum \: m \lgroup 0,1,2,4,7,8,12,14,15,16,17,18,20,24,28,30,31 \rgroup }
Solution
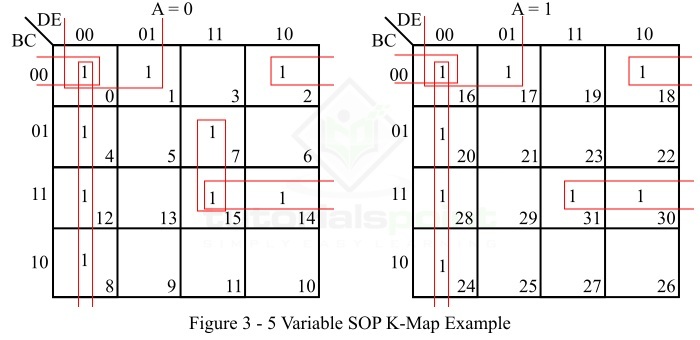
图 3 中显示了给定 SOP 布尔函数的 SOP K 图表示。
The SOP K-map representation of the given SOP Boolean function is shown in Figure 3.
Explanation
使用五变量 K 图(图 3)对给定五变量布尔函数的最小化按以下步骤进行:
The minimization of the given 5 variable Boolean function using the five variable K-map (Figure 3) is done as per the following steps −
K 映射中没有孤立的 1。
There are no isolated 1s in the K-map.
最小项 m0 可以与 m4、m8、m12、m16、m20、m24 和 m28 形成一个八正方形。因此,可以生成该项并读取为:
The minterm m0 can form an 8-square with m4, m8, m12, m16, m20, m24, and m28. So make it and read it as −
\mathrm{\lgroup \overline{D} \: \overline{E} \rgroup}
\mathrm{\lgroup \overline{D} \: \overline{E} \rgroup}
最小项 m0、m1、m16 和 m17 形成一个四正方形。生成该项并读取为:
The minterms m0, m1, m16, and m17 form a 4-square. Make it and read it as −
\mathrm{\lgroup \overline{B} \: \overline{C} \: \overline{D} \rgroup}
\mathrm{\lgroup \overline{B} \: \overline{C} \: \overline{D} \rgroup}
最小项 m0、m2、m16 和 m18 形成一个四正方形。生成该项并读取为:
The minterms m0, m2, m16, and m18 form a 4-square. Make it and read it as −
\mathrm{\lgroup \overline{B} \: \overline{C} \: \overline{E} \rgroup}
最小项 m7 和 m15 形成一个二正方形。生成该项并读取为:
The minterms m7 and m15 form a 2-square. Make it and read it as −
\mathrm{\lgroup \overline{A}CDE \rgroup}
\mathrm{\lgroup \overline{A}CDE \rgroup}
最小项 m14、m15、m30 和 m31 形成一个四正方形。生成该项并读取为:
The minterms m14, m15, m30 and m31 form a 4-square. Make it and read it as −
\mathrm{\lgroup BCD \rgroup}
\mathrm{\lgroup BCD \rgroup}
最后,以 SOP 形式编写所有积项。
Finally, write all the product terms in SOP form.
因此,给定五变量布尔函数的最小 SOP 表达式为:
Hence, the minimal SOP expression of the given 5 variable Boolean function is,
\mathrm{f(A,B,C,D,E) \ = \: \overline{A}CDE \: + \: \overline{B} \: \overline{C} \: \overline{D} \: + \: \overline{B} \: \overline{C} \: \overline{E} \: + \: BCD \: + \: \overline{D} \: \overline{E}}
Example 2
使用五变量 K 图,以 POS 形式最小化以下 5 个变量布尔函数。
Minimize the following 5 variable Boolean function in POS form using the five variable K map.
\mathrm{f \lgroup A,B,C,D,E \rgroup \: = \: \prod \: M \lgroup 3,5,6,9,10,11,13,19,21,22,23,25,26,27,29 \rgroup}
Solution
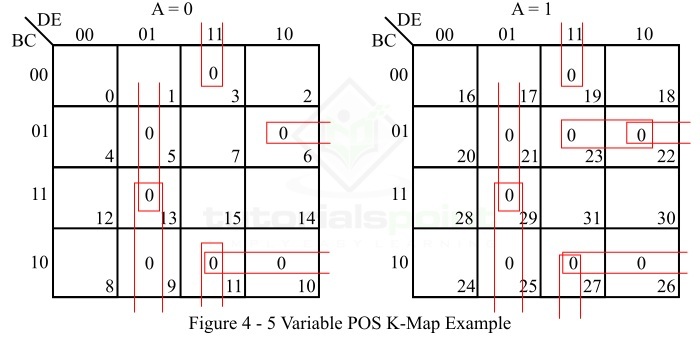
图 4 中给出了给定 POS 布尔函数的 POS K 图表示。
The POS K-map representation of the given POS Boolean function is shown in Figure 4.
Explanation
根据以下步骤使用五变量 K 图(图 4)最小化给定的 5 变量布尔函数:
The minimization of the given 5 variable Boolean function using the five variable K-map (figure-4) is done as per the following steps −
K 图中没有孤立的零。
There are no isolated zeros in the K-map.
最大项 M9、M13、M25 和 M29 形成一个 4 平方。将其作成一个方块,并将其解读为:
The maxterms M9, M13, M25, and M29 form a 4 – square. Make it and read it as −
\mathrm{\lgroup \overline{B} \: + \: D \: + \: \overline{E} \rgroup}
\mathrm{\lgroup \overline{B} \: + \: D \: + \: \overline{E} \rgroup}
最大项 M3、M11、M19 和 M27 形成一个 4 平方。将其作成一个方块,并将其解读为:
The maxterms M3, M11, M19, and M27 form a 4 – square. Make it and read it as −
\mathrm{\lgroup C \: + \: \overline{D} \: + \: \overline{E} \rgroup}
\mathrm{\lgroup C \: + \: \overline{D} \: + \: \overline{E} \rgroup}
最大项 M5、M13、M21 和 M29 形成一个 4 平方。将其作成一个方块,并将其解读为:
The maxterms M5, M13, M21, and M29 form a 4 – square. Make it and read it as −
\mathrm{\lgroup \overline{C} \: + \: D \: + \: \overline{E} \rgroup}
最大项 M6 和 M22 形成一个 2 平方。将其作成一个方块,并将其解读为:
The maxterms M6 and M22 form a 2 – square. Make it and read it as −
\mathrm{\lgroup B \: + \: \overline{C} \: + \: \overline{D} \: + \: E \rgroup}
最大项 M10、M11、M26 和 M27 形成一个 4 平方。将其作成一个方块,并将其解读为:
The maxterms M10, M11, M26, and M27 form 4 – square. Make it and read it as −
\mathrm{\lgroup \overline{B} \: + \: C \: + \: \overline{D} \rgroup}
最大项 M22 和 M23 形成一个 2 平方。将其作成一个方块,并将其解读为:
The maxterms M22 and M23 form 2 – square. Make it and read it as −
\mathrm{\lgroup \overline{A} \: + \: B \: + \: \overline{C} \ + \: \overline{D} \rgroup}
最后,以 POS 形式写出所有和式项。
Finally, write all the sum terms in POS form.
因此,给定五变量布尔函数的最小 POS 表达式为:
Therefore, the minimal POS expression of the given Boolean function in five variables is,
\mathrm{f \lgroup A,B,C,D,E \rgroup \: = \: \lgroup \overline{B} \: + \: D \: + \: \overline{E} \rgroup \lgroup C \: + \: \overline{D} \: + \: \overline{E} \rgroup \lgroup \overline{C} \: + \: D \: + \: \overline{E} \rgroup \lgroup B \: + \: \overline{C} \: + \: \overline{D} \: + \: E \rgroup \lgroup \overline{B} \: + \: C \: + \: \overline{D} \rgroup \lgroup \overline{A} \: + \: B \: + \: \overline{C} \: + \: \overline{D} \rgroup}
Numerical Problems on K-Map
为了更好地掌握五变量 K-map 的使用,以简化布尔表达式,请尝试解决以下数值问题。
Try to solve the following numerical problems to get better command on the utilization of five variable K-map to reduce a Boolean expression.
Q1. 使用 K-map,化简以下五个变量的布尔表达式成 SOP 形式。
Q1. Reduce the following five variable Boolean expression in SOP form using K-Map.
\mathrm{f \lgroup A,B,C,D,E \rgroup \: = \: \sum m \lgroup 0,3,4,6,8,10,11,12,15,17,18,22,25,26,27,30,31 \rgroup }
Q2. 使用 K-map,化简以下五个变量的布尔表达式成 POS 形式。
Q2. Reduce the following five variable Boolean expression in POS form using K-map.
\mathrm{f \lgroup A,B,C,D,E \rgroup \: = \: \prod \: M\lgroup 0,1,2,4,6,7,9,10,11,13,15,16,18,19,25,26,28,29,31 \rgroup }
Conclusion
以上便是五变量 K-map 的全部内容。从上述讨论中,我们可以得出结论,一个五变量布尔函数可以通过 5 变量 K-map 化简为最简形式。一个五变量 K-map 含有 32 个方格或单元,编号从 0 至 31。这 32 个单元被排列成两个部分,每个部分各包含 16 个单元。但是,5 变量 K-map 分割为两个部分的形式使得其在布尔函数最小化方面的应用略显复杂。
This is all about the five variable K-map. From the above discussion, we can conclude that a five variable Boolean function can be reduced to the minimal form using the 5 variable K-map. A five variable K-map has 32 squares or cells from 0 to 31. These 32 cells are arranged in two blocks 16 cells each. However, the split form of the 5 variable K-map into two blocks makes the use of it to minimize a Boolean function slightly complex.