Digital-electronics 简明教程
XOR Gate in Digital Electronics
在数字电子学中, XOR gate 是用于确定两个信号之间的差异性的派生逻辑门。
In digital electronics, the XOR gate is a derived logic gate used to determine the dissimilarity between two signals.
在本章中,我们将学习异或门的理论和操作。让我们从异或门的基本定义入手。
In chapter, we will study the theory and operation of XOR gate. Let’s get started with the basic definition of XOR gate.
What is an XOR Gate?
异或门是数字电子学中的一种逻辑门,具有两个输入和一个输出。只有当两个输入均不相同的时候,异或门的输出才为高电平或逻辑 1。对于相同的输入,异或门的输出为低电平或逻辑 0。
The XOR gate is a type of logic gate in digital electronics which has two inputs and one output. The output of the XOR gate is high or logic 1, only when both the inputs are different. For the same inputs, the output of the XOR gate is low or logic 0.
异或门也称为互斥或门或 Ex-OR 门。这种逻辑门广泛用于像加法器和减法器那样的数字算术电路中。
XOR gate is also called Exclusive OR gate or Ex-OR gate. This logic gate is widely used in digital arithmetic circuits like adders and subtractors.
由于只有在两个输入都相异的时候异或门的输出才会变高,因此它也被称为 inequality detector 。
Since the output of the XOR gate is high only when both of the inputs are dissimilar, it is also known as the inequality detector.
值得注意的是,没有三输入或多个输入的异或门。因此,当我们需要针对两个以上输入变量使用异或门时,我们会使用两个或两个以上两输入异或门。
It is very important to note that there is no such thing like three or more input XOR gate. Hence, when we need XOR gate for more than two input variables, we use two or more two-input XOR gates.
Logic Symbol of XOR Gate
异或门的逻辑符号如下图所示。
The logic symbol of an XOR gate is shown in the following figure.

它只有两个输入,指定为 A 和 B ,还有一个用 Y 表示的输出。
It has only two inputs designated as A and B and one output denoted by Y.
Truth Table of XOR Gate
异或门的真值表是一张表,它表示其输入和输出之间的关系。
The truth table of XOR gate is a table that represents the relationship between its inputs and output.
异或门的真值表如下所示 −
The truth table of an XOR gate is given below −
Inputs |
Output |
A |
B |
Y |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
从这个真值表中,我们可以看出,只有当两个输入都相异的时候,异或门的输出才为高电平或逻辑 1。当两个输入都相同时,输出为低电平或逻辑 0。
From this truth table, we can observe that the output of the XOR gate is high or logic 1 only when the both inputs are different. In the case, when both inputs are similar the output is low or logic 0.
Boolean Expression of XOR Gate
布尔表达式是一种逻辑函数,以数学方式表示异或门的输入和输出之间的关系。
The Boolean expression is a logical function that represents the relationship between inputs and output of an XOR gate mathematically.
以下等式被称为异或门的布尔表达式。
The following equation is known as the Boolean expression of the XOR gate.
\mathrm{Y \: = \: A \oplus B}
此方程式也可表示为以下形式 −
This equation can also be expressed as below −
\mathrm{Y \: = \: AB' \: + \: A’B \: = \: A \bar{B} \: + \: \bar{A}B}
\mathrm{Y \: = \: AB' \: + \: A’B \: = \: A \bar{B} \: + \: \bar{A}B}
此处,符号“$\mathrm{\oplus}$”表示 XOR 运算。
Here, the symbol "$\mathrm{\oplus}$" denotes the XOR operation.
Working of XOR Gate
下面介绍不同输入组合的 XOR 门的详细工作原理 −
The detailed working of XOR gate for different input combinations is explained below −
-
If A = 0 and B = 0, the output of the XOR gate is Y = 0.
-
If A = 0 and B = 1, the output of the XOR gate is Y = 1.
-
If A = 1 and B = 0, the output of the XOR gate is Y = 1.
-
If A = 1 and B = 1, the output of the XOR gate is Y = 0.
从这个解释中,我们可以看到 XOR 门的输出只有在输入不同时才会变为高电平或逻辑 1。
From this explanation, we can see the output of XOR gate is high or logic 1 only when inputs are dissimilar.
XOR Gate as an Inverter
XOR 门还可以用作反相器。XOR 运算有一种属性,即
The XOR gate can also be used as an inverter. There is a property of XOR operation that is,
\mathrm{A \: \oplus \: 1 \: = \: \bar{A}}
因此,通过利用此属性,我们可以得出这样的结论:如果 XOR 门的一个输入线上连接到逻辑 1,并将输入信号应用到另一输入线上。然后,XOR 门将应用信号的反相版本产生为输出。
Hence, by utilizing this property, we can state that if one of the input lines of the XOR gate is connected to logic 1 and the input signal is applied to another input line. Then, the XOR gate produces the inverted version of the applied signal as the output.
下图显示了 XOR 门作为反相器时的操作。
The following figure shows the operation of XOR gate as an inverter.
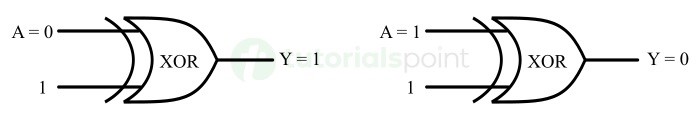
XOR Gate as a Buffer
缓冲器门是一种产生与输入相同的输出的逻辑门。它用来在输入和输出之间提供一些延迟。
A buffer gate is a logic gate that produces the same output as the input. It is used to provide some delay in the input and output.
XOR 逻辑有一种属性,即
There is a property of XOR logic that is,
\mathrm{A \: \oplus \: 0 \: = \: A}
因此,如果 XOR 门的两条输入线中的一条连接到逻辑 0,并且将输入信号应用到另一条输入线上。然后,XOR 门会产生与输入相同的输出。
Hence, if one of the two input lines of the XOR gate is connected to a logic 0 and the input signal is applied to another input line. The XOR gate then produces the output same as the input.
XOR 门作为缓冲器逻辑的操作在以下图形中说明。
The operation of the XOR gate as a buffer logic is illustrated in the following figure.
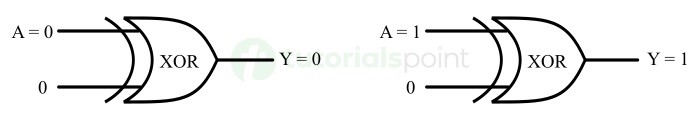
XOR Gate using Switches
我们还可以使用电池、两个简单的开关和一个灯来实现 XOR 门逻辑。
We can also implement the XOR gate logic using a battery, two simple switches, and a lamp.
下图中描绘了用开关搭建的异或门电路图。
The following figure depicts the circuit diagram of the XOR gate using switches.
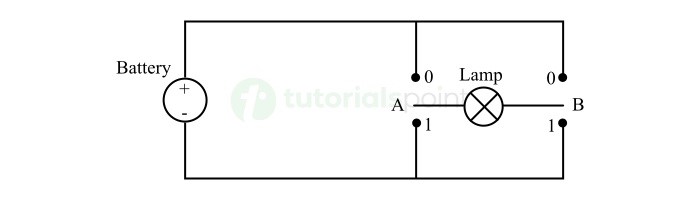
在这个开关电路中,如果开关 A 和 B 处于同等级别(0 或 1),灯泡将不会点亮。此状态代表低或逻辑 0 输出。
In this switching circuit, if the switches A and B are on the same level (either 0 or 1), the lamp will not glow. This state represents the low or logic 0 output.
如果开关 A 和 B 处于不同级别,即, A 为 0 且 B 为 1 或 A 为 1 且 B 为 0。那么,我们可以看到有一个闭路供电流流经灯泡,从而让灯泡亮起。这代表高或逻辑 1 输出。
If the switches A and B are at different levels, i.e., A is at 0 and B is at 1 or A is at 1 and B is at 0. Then, we can see there is a closed path for current to flow through the lamp, making the lamp turn on. This represents the high or logic 1 output.
因此,以上所示电路实施异或逻辑函数。
Hence, the above shown electrical circuit implements the XOR logic function.
Applications of XOR Gate
以下是一些异或门的关键应用——
The following are some key applications of the XOR gate −
-
XOR gate is used in computational and arithmetic circuits like adders, subtractors, etc.
-
XOR gate is used to detect errors, similarities and dissimilarities between two logic levels or signals.
-
XOR gate is used as a controlled inverter or buffer logic.
Conclusion
总之,异或门是一个双输入和单输出逻辑门,当施加在其上的输入不相同时,产生一个高或逻辑 1 输出。
In conclusion, the XOR gate is a two input and one output logic gate that produces a high or logic 1 output when the inputs applied to it are dissimilar.
异或门逻辑广泛用于楼梯电线和许多其他自动化电路中,其中一个设备(如灯)必须由两个不同的位置控制。
The XOR gate logic is widely used in staircase electric wiring and many other automation circuits, where a single device like lamp has to be controlled from two different locations.