Digital-electronics 简明教程
Gray Code to Binary Converter
格雷码到二进制转换器是一种可以将格雷码转换为等效的纯二进制码的数字电路。因此,格雷码到二进制转换器以格雷码作为输入,并输出纯二进制码。
A gray code-to-binary converter is a digital circuit that can translate a gray code into an equivalent pure binary code. Thus, a gray code to binary converter takes a gray code as input and gives a pure binary code as output.
下面给出了 3 位格雷码到二进制码转换器的真值表 −
The truth table of a 3-bit gray code to binary code converter is given below −
Gray Code |
Binary Code |
G2 |
G1 |
G0 |
B2 |
B1 |
B0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
让我们获得二进制输出位的布尔表达式。为此,我们将使用 K 映射技术简化真值表。
Let us obtain the Boolean expression for the binary output bits. For this, we will simplify the truth table using the K-map technique.
K-Map for Binary Bit B0
图中显示了二进制输出位 B0 的 K 映射简化。
The K-map simplification for the binary output bit B0 is shown in the following figure.
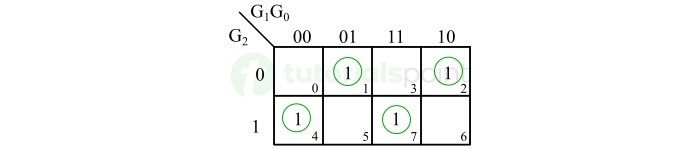
二进制位 B0 的布尔表达式为:
The Boolean expression for the binary bit B0 will be,
\mathrm{B_{0} \: = \: \overline{G_{2}} \: \overline{G_{1}} \: G_{0} \: + \: \overline{G_{2}} \: G_{1} \: \overline{G_{0}} \: + \: G_{2} \: \overline{G_{1}} \: \overline{G_{0}}\: + \: G_{2} \: G_{1} \: G_{0}}
我们还可以进一步简化此表达式,如下所示:
We can further simplify this expression as follows,
\mathrm{\Rightarrow \: B_{0} \: = \: \overline{G_{2}} \: (\overline{G_{1}} \: G_{0} \: + \: G_{1} \: \overline{G_{0}}) \: + \: G_{2} \: (\overline{G_{1}} \: \overline{G_{0}}\: + \: G_{1} \: G_{0})}
\mathrm{\Rightarrow \: B_{0} \: = \: \overline{G_{2}} \: ( G_{0} \: \oplus \: G_{1}) \: + \: G_{2} \: \overline{(G_{0} \: \oplus \: G_{1})}}
\mathrm{B_{0} \: = \: G_{0} \: \oplus \: G_{1} \: \oplus \: G_{2}}
以下是二进制位 B0 的简化表达式。
This is the simplified expression for the binary bit B0.
K-Map for Binary Bit B1
K-map 对二进制输出 B1 的简化如下所示。
The K-map simplification for the binary output B1 is shown below.
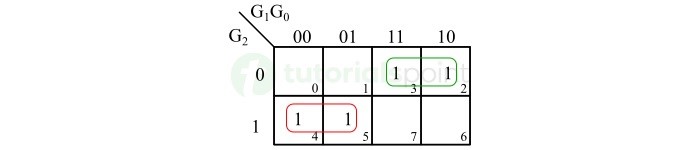
二进制位 B1 的布尔表达式为:
The Boolean expression for the binary bit B1 is,
\mathrm{B_{1} \: = \: G_{2} \: \overline{G_{1}} \: + \: \overline{G_{2}} \: G_{1} \: = \: G_{1} \: \oplus \: G_{2}}
K-Map for Binary Bit B2
下图显示了对二进制位 B2 的 K-map 简化。
The following figure shows the K-map simplification for the binary bit B2.
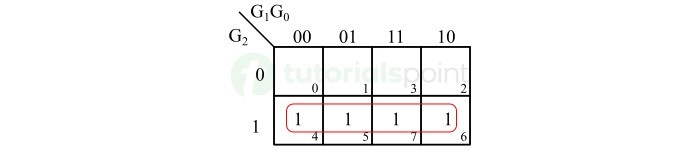
从这个 K-map 中,我们得到以下布尔表达式:
From this K-Map, we obtain the following Boolean expression −
\mathrm{B_{2} \: = \: G_{2}}
这种 3 位格雷码到二进制码转换器的逻辑电路实现如下图所示。
The logic circuit implementation of this 3-bit gray to binary code converter is shown in the following figure.
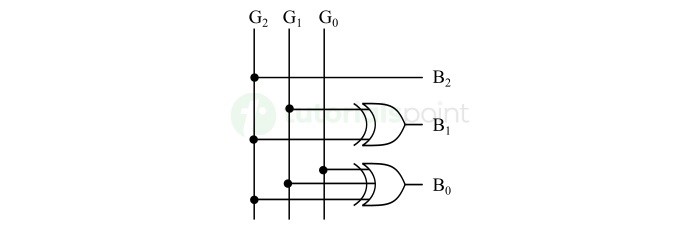
该逻辑电路能够将 3 位格雷码转换为等效的 3 位二进制码。我们也可以遵循相同的过程实现针对任何位数的格雷码到二进制码转换器。
This logic circuit can translate a 3-bit gray code into an equivalent 3-bit binary code. We can also follow the same procedure to implement a gray code to binary code converter for any number of bits.