Digital-electronics 简明教程
Digital Electronics - Half Subtractor
在数字电子学中, subtractor 是可以执行两个数(二进制数)相减并生成它们之间的差值的组合逻辑电路。这是一个组合电路,这意味着其输出仅依赖于其当前输入。尽管在实践中,两个二进制数的相减是通过计算被减数的 1 的或 2 的补码,并将其加到被减数上而完成的。
In digital electronics, a subtractor is a combinational logic circuit that can perform the subtraction of two number (binary numbers) and produce the difference between them. It is a combinational circuit that means its output depends on its present inputs only. Although, in practice, the subtraction of two binary number is accomplished by taking the 1’s or 2’s compliment of the subtrahend and adding it to the minuend.
通过这种方式,二进制数的相减操作可以转换为简单的相加操作,这使得硬件构建既简单又便宜。减法器有两种类型,即 Half Subtractor 和 Full Subtractor 。
In this way, the subtraction operation of binary numbers can be converted into simple addition operation which makes hardware construction simple and less expensive. There are two types of subtractors namely, Half Subtractor and Full Subtractor.
在本文中,我们将讨论半减法器及其基本定义、电路图、真值表、特性方程等。因此,让我们从半减法器的基本定义开始。
In this article, we will discuss the half subtractor, its basic definition, circuit diagram, truth table, characteristic equation, etc. So let’s begin with the basic definition of half subtractor.
What is a Half-Subtractor?
half-subtractor 是一个有两个输入和两个输出(即差值和借位)的组合逻辑电路。半减法器产生输入端两个二进制位之间的差值,并产生借位输出(如果有)。在减法 (A-B) 中,A称为 Minuend bit ,B称为 Subtrahend bit 。半减法器的框图和逻辑电路图如图 1 所示。
A half-subtractor is a combinational logic circuit that have two inputs and two outputs (i.e. difference and borrow). The half subtractor produces the difference between the two binary bits at the input and also produces a borrow output (if any). In the subtraction (A-B), A is called as Minuend bit and B is called as Subtrahend bit. The block diagram and logic circuit diagram of the half subtractor is shown in Figure-1.
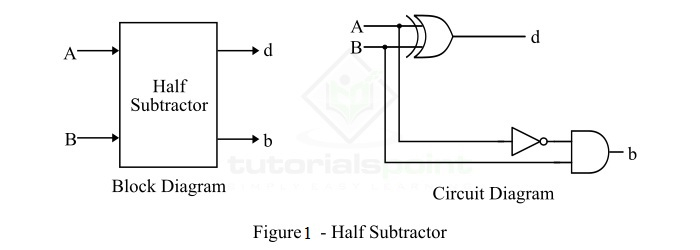
因此,从逻辑电路图中可以看出,可以使用 XOR 门与 NOT 门和 AND 门一起实现半减法器。
Hence, from the logic circuit diagram, it is clear that a half subtractor can be realized using an XOR gate together with a NOT gate and an AND gate.
在如图 1 所示的半减法器中,A 和 B 是输入,d 和 b 是输出。其中,d 表示差值,b 表示借位输出。借位输出 (b) 是告诉下一级已经借用 1 的信号。
In the half subtractor as shown in figure-1, A and B are the inputs, d and b are the outputs. Where, d indicates the difference and b indicates the borrow output. The borrow output (b) is the signal that tells the next stage that a 1 has been borrowed.
Operation of Half Subtractor
现在,让我们了解半减法器电路的工作原理。半减法器根据二进制减法的规则执行其操作以找出两个二进制位之间的差值,如下所示 −
Now, let us understand the operation of the half subtractor circuit. Half subtractor performs its operation to find the difference of two binary digits according to the rules of binary subtraction, which are as follows −
只要被减数位 (A) 大于或等于被减数位 (B),即 A ≥ B,输出借位 b 为零 (0)。当 A = 0 且 B = 1 时,输出借位为 1。
The output borrow of b is zero (0) as long as the minuend bit (A) is greater than or equal to the subtrahend bit (B), i.e. A ≥ B. The output borrow is a 1 when A = 0 and B = 1.
从半减法器的逻辑电路图中可以看出,差值位 (d) 由两个输入 A 和 B 的 XOR 运算获得,借位由被减数 (A') 与被减数 (B) 的补码进行 AND 运算获得。
From the logic circuit diagram of the half subtractor, it is clear that the difference bit (d) is obtained by the XOR operation of the two inputs A and B, and the borrow bit is obtained by AND operation of the compliment of the minuend (A') with the subtrahend (B).
Truth Table of Half Subtractor
以下是半减法器的真值表−
The following is the truth table the half-subtractor −
Inputs |
Outputs |
A |
B |
D (Difference) |
B (Borrow) |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
K-Map for Half Subtractor
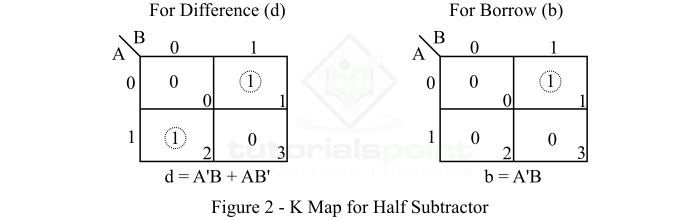
我们可以使用 K 映射(或卡诺图),这是一种简化布尔代数的方法,来确定差值位 (d) 和输出借位 (b) 的方程。
We can use the K-Map (or Karnaugh Map), a method for simplifying Boolean algebra, to determine equations of the difference bit (d) and the output borrow (b).
半减法器的 K-Map 简化如图 2 所示。
The K-Map simplification for half subtractor is shown in Figure-2.
Characteristic Equation of Half Subtractor
半减法器的特性方程,即差值位 (d) 和输出借位 (b) 的方程是通过遵循二进制减法的规则获得的。这些方程表示如下 −
The characteristic equations of the half subtractor, i.e. equations of the difference bit (d) and the output borrow bit (b) are obtained by following the rules of binary subtraction. These equations are given as follows −
半减法器的差位 (d) 由 XORing 两个输入 A 和 B 得到。因此,
The difference bit (d) of the half subtractor is given by XORing the two inputs A and B. Therefore,
\mathrm{差值, \: d \: = \: A \oplus B \: = \: A’B \: + \: AB'}
\mathrm{Difference, \: d \: = \: A \oplus B \: = \: A’B \: + \: AB'}
半减法器的借位 (b) 是 A'(A 的补码)和 B 的 AND。因此,
The borrow (b) of the half subtractor is the AND of A’ (compliment of A) and B. Therefore,
\mathrm{借位, \: b \: = \: A’B}
\mathrm{Borrow, \: b \: = \: A’B}
Applications of Half Subtractor
减法器的一些重要应用如下:
The following are some important applications of half subtractor −
-
Half subtractor is used in ALU (Arithmetic Logic Unit) of processors.
-
Half subtractor can also be used in amplifiers to compensate the sound distortion.
-
It is also used to decrease the force of radio signals or audio signals.
-
Half subtractor is also used to increase or decrease operators.
Conclusion
通过上述讨论,我们可以得出结论,减法器是一种组合逻辑电路,可计算两个二进制数的差值。当某一进制数减去另一进制数时,减法器只能用于减去被减数的最低有效位 (LSB) 减去减数的 LSB。
From the above discussion, we can conclude that a half subtractor is a combinational logic circuit that can calculate the difference of two binary digits. A half subtractor can only be used to subtract the LSB (Least Significant Bit) of the subtrahend from the LSB of the minuend when one binary number is subtracted from another binary number.